Watch this lab’s video walkthrough

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

This lab will help you solidify your understanding of dynamic arrays by having you implement your own dynamic array. We will also cover amortized analysis and discuss why it is important.

---

Background Info

We use the word dynamic in two different ways. Please pay attention to the difference between the two:

1. Dynamic allocation means allocating memory at run time instead of compile time. This happens with the use of the new keyword.
2. Dynamic arrays, or vectors, are arrays that automatically change size by growing or shrinking as necessary. This is the main focus of this lab.

Static Arrays

Arrays are one of the most common and versatile data structures and are essential to almost any useful C or C++ program. They allow us to store hundreds, or even thousands, of elements inside of memory while providing random access in O(1) to all of them. While these helpful structures provide us with near-instant access to our data whenever we need it, they are not without weakness. When using regular C-style arrays, you must declare a fixed size for them at the time of their creation and, once this size is declared, it cannot be changed.

// this array is limited to a maximum of 100 elements, it CANNOT hold more
int myArray[100];
// this array is dynamically *allocated* but its size is still static
int *myOtherArray = new int[100];

This presents a problem: What if you don’t know how much space you need in your array at compile time? On one hand, if you declare an array with too little space, you will have nowhere to store additional values. On the other hand, if you always declare an array with maximum capacity (e.g. ULLONG_MAX equal to 18446744073709551615) you will almost certainly have enough space, but you will be wasting huge amounts of unused memory in almost any situation.

As it turns out, the solution to the problem of capacity is to use Dynamic Arrays, or vectors (as they are known in C++).

Dynamic Arrays (Resizable Arrays)

Dynamic Arrays are similar to regular C++ arrays in that they still provide random access in constant time to elements. However, Dynamic Arrays have the advantage of being dynamically resizable. This means that they can grow as you add more elements to them and shrink as you no longer need space. Using a Dynamic Array, you don’t need to know the size of a list at compile time.

The way a Dynamic Array works is to begin with a starting size (often 0). For every insert, we do one of two things depending on the current state of the array:

If array is NOT full:
	insert into our array 
If array IS full:
	dynamically allocate memory for new array
	copy data from old array into new array
	delete the old array

Analyzing Dynamic Arrays

Assuming you have enough space to add an element to a static array, what is the time complexity of inserting into a static array? (after giving it some thought, click to reveal answer)

For static arrays, an insert operation runs in O(1) (i.e., constant) time. Since we have random memory access, and all of the space we need is already allocated, we simply need to index into the appropriate index and assign it the value we are inserting. It does not matter if we are inserting into index 0, or index 10,000-- both operations will take the same amount of time.

But what about for a Dynamic Array? If we have enough space as-is, inserts will take O(1) time, but inserts that require resizing will take longer.

What is the time complexity of inserting into a dynamic array when it requires resizing the array? (after giving it some thought, click to reveal answer)

Recall that if a dynamic array is full, thwe following steps must be performed: 1. dynamically allocate memory for new array 2. copy data from old array into new array 3. delete the old array Step one is assignment-- that's constant time. Step 2 requires that we access each element in the old array and then access and assign it to the new array. Assuming our old array is size n, we will need to perform linear (i.e., O(n)) work since we have to do some amount of work for each element. Lastly, step 3 is the opposite of assignment so it's also constant time. Since linear work (O(n)) is higher order than constant work O(1), inserting into a dynamic array when it requires resizing the array is O(n).

Observe the following series of inserts:

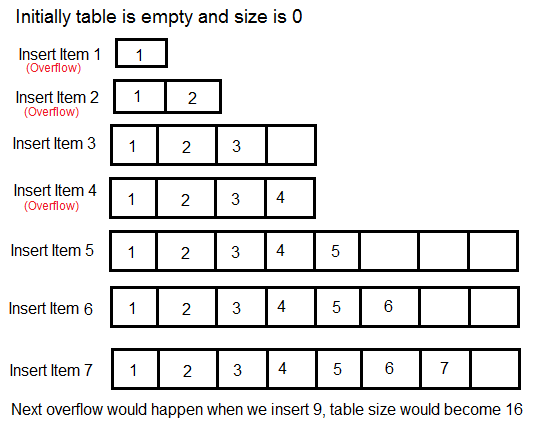
Any time there is the (Overflow) label, that is saying the array must be resized. How can we calculate the run time for a function (insert) that is sometimes O(1), and sometimes O(n)?

• If we’re trying to do worst-case and we assume every time we insert we need to resize the array we get O(n)
• If we’re trying to do best-case and we assume every time we insert we do not need to resize the array we get Ω(1)
• Given that worst case is O(n) and best case is Ω(1), there is no Θ (recall that a function T(n) is Θ(f(n)) if and only if it is O(f(n)) and Ω(f(n))).

Well neither of those helpful! There’s no Theta and the way we know how to calculate Big-O and Big-Omega give us run-times that are too different to give us any useful information. This is where amortized analysis comes in. For functions that can behave so drastically different, we take the average run time over a series of several runs. In our case, let’s take that over a series of n insertions: say half of them take constant time and the other half takes linear time. We add up all the costs and divide by how many total insertions there were as shown in the image below:

With amortized analysis, we see that on average, inserting into a dynamic array will be constant time or O(1).

Despite the use of the word average, amortized analysis and average-case (Θ) are completely different. Amortized analysis is a way or means to get a time complexity, Theta is an asymptotic notation that tells us the average function behaviour as n gets very large. For more info:

• Read Big Theta and Asymptotic Notation Explained
• Read What is amortized analysis of algorithms?
• Read What is the relationship between amortized run time and big-Θ run time?

---

Your Task

Do not use a vector at all for this assignment– you are implementing a vector

The instructions below will walk you through implementing and testing your own dynamic array.

Watch this lab’s video walkthrough

1. Download the files below (it’s easiest if you right click and then choose download or save)

   DynamicArray.h

   Contains the declaration of the Dynamic Array you’ll be implementing. Do not alter any of the given private variables, public function signatures or implementations. Curious about ifndef vs pragma once? Read about their differences– the TLDR version is that while they are used for the same purpose, they work in different ways. ifndef ignores duplicates by checking that you have not defined something before anywhere, pragma once ignores duplicates by checking that you have not included the same file.

   DynamicArray.cpp

   Contains the definition of the Dynamic Array you’ll be implementing. Some functions have already been implemented for you– do not change them. The rest of the functions are up to you to implement, specifically where you see // TODO comments. You may add your own private helper functions should you wish. A helper function is a function that performs a subtask but may not necessarily be useful to others when using the class itself. For example, you might find it useful to write a function to handle the resizing of the array since you’ll be resizing in multiple places but the resize function should be hidden from users as they shouldn’t need to worry aout resizing. Therefore, you can add the resizing function as a private function of the DynamicArray class so we know it exists and is used but can’t be used outside of the class.

   test.cpp

   Contains some tests that should pass as soon as you download the code, without you having to change anything, as well as some tests that should pass after you have completed the tasks below. You should add your own test cases to this file.

   doctest.h

   The library we’ll be using for our own automated tester. There’s a ton of code in here so don’t worry too much about understanding everything it does– just know the library is extremely powerful and we’ll only be scratching the surface of everything it can do. Do not edit this file.

2. Once you have downloaded all the files, inspect them. Ask questions if you have them.
3. Create your own makefile to compile and run your program. Refer to Lab 3 as needed.
4. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in.
5. Implement and test the overloaded constructors

   Note: You should initialize all member variables in all constructors so you don’t end up with any garbage values.

6. Implement and test append() and prepend()

   Notes:

   • If the array is empty to begin with, increase its capacity to 1, otherwise, if, the array is full, you should increase its capacity by the scaling factor.
   • Recall the algorithm for inserting into an an array:

      If array's capacity is 0 or if array does not exist:
        Increase capacity to 1
        dynamically allocate memory for new array
      Otherwise, if array is full:
        Increase capacity by the scaling factor
        dynamically allocate memory for new array (make sure you don't accidentally overwrite m_data)
        copy data from old array (array pointed to by m_data) into new array
        delete the old array (delete array pointed to by m_data, then reassign m_data to point to the new array)
      Insert new value into array
      Increment m_length by 1
     

7. Implement and test findFirstOf() and findLastOf()
8. Implement and test removeLast(), removeFirst(), and clear()

   Note: the array should decrease its capacity by the scaling factor whenever it’s been emptied to 1/(2 x m_scaling_factor) its capacity or less (i.e., if the scaling factor is 2, the array should shrink to 1/2 its size when it’s 1/4 full or less; if the scaling factor is 5, the array should shrink to 1/5 its size when it’s 1/10 full or less)

Watch this lab’s video walkthrough

---

Requirements

Your submission will be tested and graded by an autograder, for this reason it cannot be stressed enough that your program must exactly follow the assignment specifications:

1. Makefile implemented correctly
2. Overloaded constructors implemented correctly
3. append() and prepend() implemented correctly, as specified
4. findFirstOf() and findLastOf() implemented correctly
5. removeLast(), removeFirst(), and clear() implemented correctly, as specified

---

Handing in

To submit your solution to Gradescope, select all of the following files and use the drag and drop option:

• DynamicArray.h
• DynamicArray.cpp
• makefile
• test.cpp

---

Grade Breakdown

You must successfully meet requirement 1 through 5 in order to receive credit for this assignment.

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

---

Original assignment by Dr. Marco Alvarez, modified assignment version by Christian Esteves, used and modified (again) with permission.