URI CSC 212 logo URI CSC 212

Lab 6

Basic Sorting Algos

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

This lab will help you solidify your understanding of the implementation and analysis of basic sorting algos.

Background Info

Stable vs Unstable Sorting
Stable Unstable
Preserves original order relative order of elements Doesn’t preserve original order relative order of elements
Necessary when equal elements are not truly equal Okay to use if equal elements are truly equal or if working with no repeats
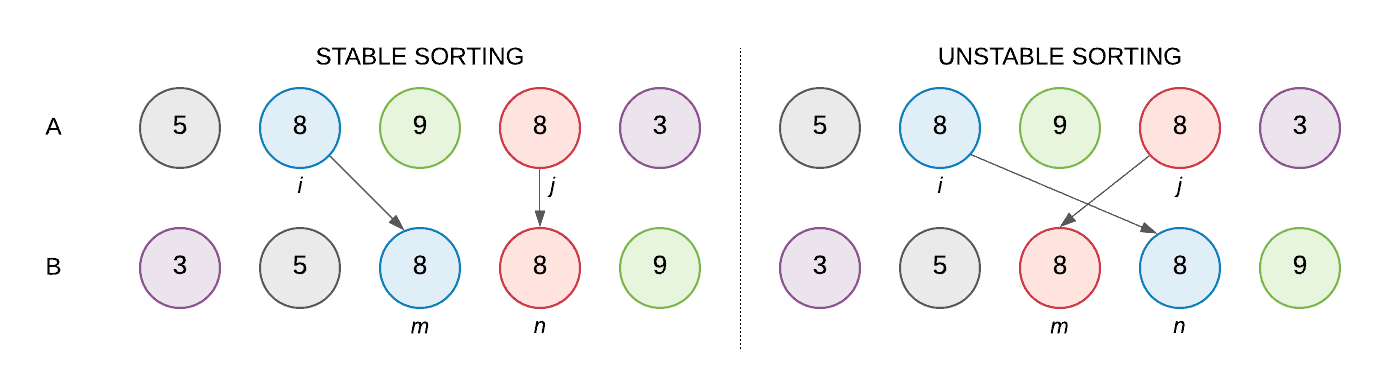
image showing example of stable vs unstable sorting using colored and numbered balls
I have two students with the same first and last name. I want to sort my roster by name and GPA, and I need to make sure the grades don't accidentally get switched. Should I use stable or unstable sorting? (after giving it some thought, click to reveal answer) Since I need to make sure the grades don't accidentally get switched, I need to make sure that when I sort my roster, the names stay in the correct relative order. This means I should use a stable sorting algo .


I have two students with the same first and last name. I want to sort my roster by ID, and I need to make sure the grades don't accidentally get switched. Should I use stable or unstable sorting? (after giving it some thought, click to reveal answer) Since ID numbers are unique, I can use an unstable sorting algo .


A cashier is sorting the bills in their register. Should they use stable or unstable sorting? (after giving it some thought, click to reveal answer) Since a $10 bill is the same as any other $10 dollar bill, relative order doesn’t matter. This means the cashier can use an unstable sorting algo .


Bubble Sort
Algorithm (assuming ascending order)
For every element in the list:
	Compare the current element in the list with the element immediately to its right
		If the current element is greater than the element immediately to its right, swap the two elements
After the above is performed once, the largest element in the list will be in the correct place. 
	Since we have n elements, we have to do the algorithm above n times
An example of bubble sort. Starting from the beginning of the list, compare every adjacent pair, swap their position if they are not in the right order (the latter one is smaller than the former one). After each iteration, one less element (the last one) is needed to be compared until there are no more elements left to be compared.
Big-O

In the pre-readings you saw the Counting-version analysis and the High-level analysis. Below is an Intuitive analysis:

Worst case is list in reverse order
Every element is out of order so I need to bubble each element all the way to the end, comparing it to every other element along the way. This means that for every element in an array of size n, I’m doing n work (n-1 comparisons), so this is n^2 work
Insertion Sort
Algorithm (assuming ascending order)
Start at the front of the list
Compare the current element to the element immediately to its left 
	If the current element is smaller than the element immediately to its left, compare the current element to all the other elements to the left
		- Do this until the current element is not smaller than the element its being compared to
		- Shift all greater values 1 space to the right
		- Insert the current element at the gap left from shifting
A graphical example of insertion sort. The partial sorted list (black) initially contains only the first element in the list. With each iteration one element (red) is removed from the 'not yet checked for order' input data and inserted in-place into the sorted list.
Big-O

In the pre-readings you saw the Counting-version analysis and the High-level analysis. Below is an Intuitive analysis:

Worst case is list in reverse order
Every element will be smaller than the all the ones to its left so for every element, I’m going to have to compare it to every other element. This means that for every element in an array of size n I’m doing n work (n-1 comparisons), so this is n^2 work
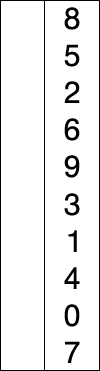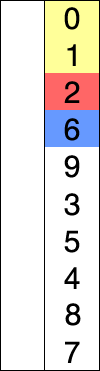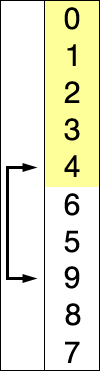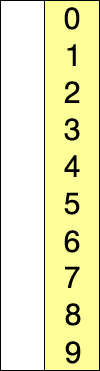
Selection Sort
Algorithm (assuming ascending order)
1. Set the current sorted_pos to 0
2. Find the smallest element in the rest of list
3. Swap the smallest element in the list with the element at sorted_pos
4. Increment sorted_pos by 1
5. Repeat 2-4 until list is sorted (until sorted_pos is n-1)
Selection sort animation. Red is current min. Yellow is sorted list. Blue is current item.
Big-O

In the pre-readings you saw the Counting-version analysis. Below is a High-level analysis and an Intuitive analysis.

High-Level Analysis Outer loop goes from 0 to n-1 and Inner loop will start at sorted_pos+1 and loop n-1 times

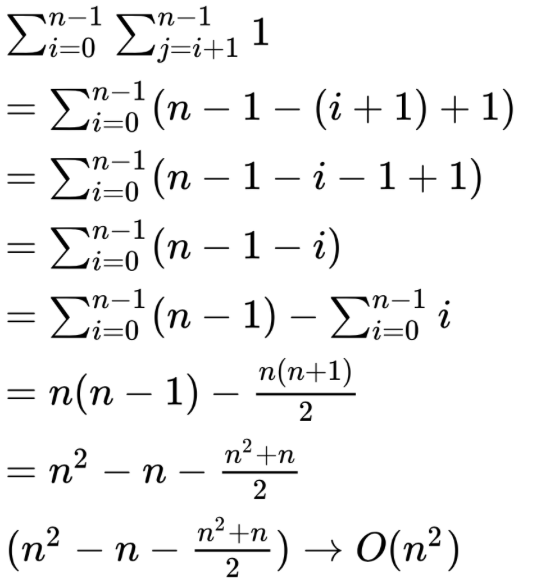
image of summations for doing big-o analysis for selection sort

Intuitive Analysis

Worst case is list in reverse order
Smallest element is at last position so for every element in the list I have to visit every other remaining element in the list. This means that for every element in an array of size n I’m doing n work (n-1 swaps), so this is n^2 work

Your Task

  1. Explore (and bookmark for later) Sorting animations of various sorting algorithms

  2. Download the files below (it’s easiest if you right click and then choose download or save)

    sorting-lab.h
    Contains the declaration of the sorting lab you’ll be implementing. Do not alter any of the given private variables, public function signatures or implementations. Curious about ifndef vs pragma once? Read about their differences– the TLDR version is that while they are used for the same purpose, they work in different ways. ifndef ignores duplicates by checking that you have not defined something before anywhere, pragma once ignores duplicates by checking that you have not included the same file.
    sorting-lab.cpp
    Contains the definition of the sorting lab you’ll be implementing. Some functions have already been implemented for you– do not change them.
    test.cpp
    Contains some tests that should pass as soon as you debug the code. You should add your own test cases to this file.
    doctest.h
    The library we’ll be using for our own automated tester. There’s a ton of code in here so don’t worry too much about understanding everything it does– just know the library is extremely powerful and we’ll only be scratching the surface of everything it can do. Do not edit this file.
    makefile
    File used to compile and run your program with the test suite.
  3. Read the code comments closely– code is supposed to follow the algorithm as written in the background info above
  4. Find (and fix) the TWO bugs
    • Note/Hint: There is one in selectionSort() and one in insertionSort()
    • Hint: You should NOT be adding any code to fix the bug– you should only be making a single small edit to a single line for each bug.
  5. Identify the step the error was in the algorithm, as written on the slides
  6. Write down how to fix it and how you knew (I recommend you type it so you can copy/paste into Gradescope)

Requirements

Your submission will be manually checked to ensure it meets the following specifications:

  1. Correct identification of step in selection sort algorithm bug is in
  2. Correct identification of how to fix bug in selection sort
  3. Correct identification of step in insertion sort algorithm bug is in
  4. Correct identification of how to fix bug in insertion sort

Handing in

Submit your answers to the questions on the Lab 6: Basic Sorting Algos assignmetn on Gradescope.

Grade Breakdown

You must successfully meet requirement 1 through 4 in order to receive credit for this assignment.

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.