Recursive Backtracking

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide you some experience with recursive backtracking. You’ll be doing this by way of implementing your own Tic Tac Toe game with an AI.

Background Info

Recursion is the practice of breaking a complicated problem down into small, trivially solvable pieces, and then merging those pieces together to solve the full problem completely. Recursive backtracking however, takes this process to the next level. This method will allow us to discard incorrect pieces & attempt to re-solve that part of the problem with different parameters.

A Lesson on Backtracking

Backtracking is a systemic method to iterate over all possible configurations of a search space. The general idea is:

) Is the task complete? Return true if so.
) At any given step, enumerate all possible actions.
2.) Make one of the enumerated actions
3.) Evaluate the new partial solution. If we obtain 'True', also return 'True' else try a different action
) If we run out of moves, return 'False' to backtrack to a previous stage of the problem

Let’s take a look at an example; solving a game of Sujiko!

The purpose of this game is to place the numbers 1-9 on the board such that the sum of the four numbers around a circle equal the number in a circle. How would you solve this puzzle?

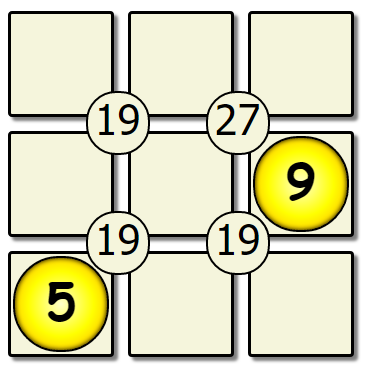
Lets take a look at an algorithm:

) Is the win condition met? If so, return true. Otherwise, continue on.
) At any given step, record all of the missing values.
2) Place the first missing value into the first open spot on the board.
3) Recursively call this function with the new board. If we obtain True, also return True. 
	     Otherwise, replace the number with the next missing value.
) If we tried all of the missing values & none worked, return False so the previous version of this board can try another number.

Lets try applying this algorithm to our board:

First Pass	Second Pass	Seventh Pass

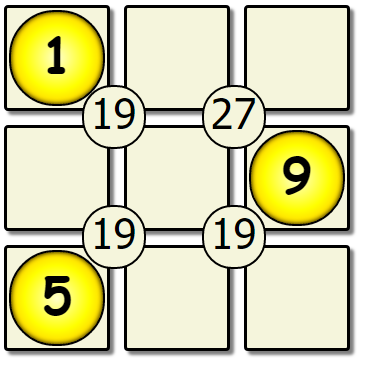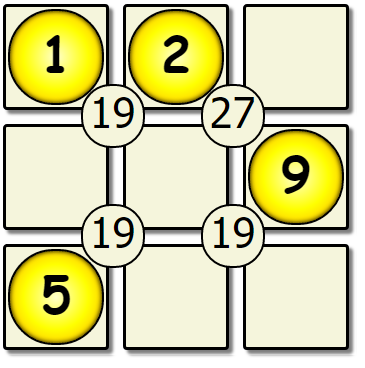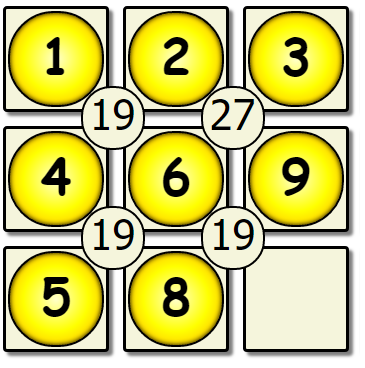
We’ve hit our first dead end, & there are no more missing values to place. This solution is not correct, so we backtrack to the previous version of the board, and change the number that was placed.

Sixth Pass Revisited	Sixth Pass Modified	Seventh Pass Revisited

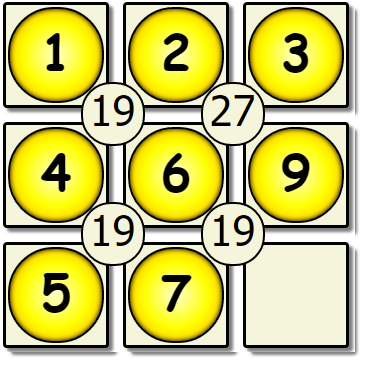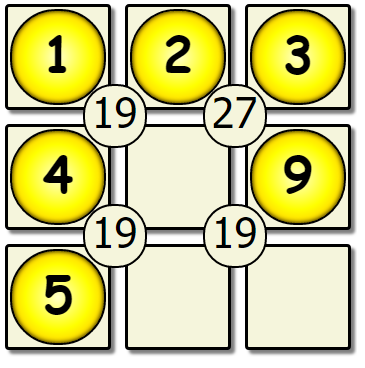
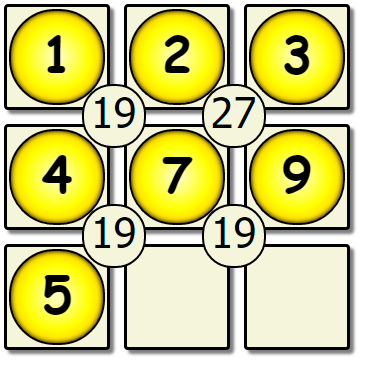
This yields another dead end, so we would backtrack back to the 5th empty spot, and change the value there.

Fifth Pass Revisited	New Fifth	New Sixth Pass

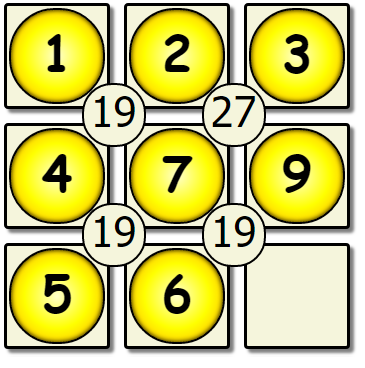This process would repeat until we have a solution board:

Tic Tac Toe

Tic tac toe (ttt), also known as ‘noughts and crosses’ or ‘Xs and Os’ is a 2 player game that involves trying to get three marks in a horizontal, vertical, or diagonal row. In ttt, players alternate turns marking a 3x3 grid with either an X (for player 1) or an O (for player 2). The first to get 3 in a row wins and if no one gets three in a row and the grid gets filled up, then the game is over with a tie.

tic tac toe game Image source

If you haven’t played ttt (ever or in a while), I recommend you take a piece of paper and do a couple of rounds with a roommate or relative. You can also play one of the many online versions against a fellow human or an AI!

Minimax Algorithm

Minimax is an algorithm used in game theory for two-player, sequential, finite-action, deterministic, zero-sum games of perfect information. Breaking down what that means:

Two-player: A game that has two players. Tic-tac-toe is a two-player game; hearts is not.
Sequential: A game in which only one player moves at a time. Monopoly is a sequential game; Rochambeau (i.e., rock-paper-scissors) is not.
Finite-action: A game in which there is a finite number of legal moves available to a player when it is his turn to move. Battleship is a finite-action game; soccer is not.
Deterministic: A game that does not depend at all on chance. Its progress is entirely a function of selected moves. Checkers is deterministic; backgammon is not.
Zero-sum: A game in which what is good for one player is equally bad for the other, and vice versa. All the examples given here are zero-sum games.
Perfect
information: A game in which both players witness the entire progression of the game. Chess is a game of perfect information; poker is not.

Given that tic-tac-toe meets all of those criteria, we can use the minimax algorithm to determine an optimal move given the following information: the player we are optimizing for and the current board at which the player will make their next move. We will refer to this data as the game’s state.

Given a game state, minimax will create a game tree whose minimax value can evaluate to either a -1, 0, or 1. A -1 denotes a winning condition for MIN, 0 denotes a tie, and a 1 denotes a winning condition for MAX. The minimax value of a game tree is the value of the root node x, whenever Min moves first, computed as the minimum value of x’s successors, which are in turn computed as the maximum value of x’s successors’ successors, and so on. Because the minimax algorithm is recursive, it searches smaller and smaller game trees with each recursive call.

Even for such a small game as Tic Tac Toe, calculating the whole game tree is computationally expensive. Therefore, we will limit our minimax algorithm using MAX_DEPTH.

if the board of the current game state is terminal (i.e., the game is over with that board):
    return the value of the board
    
update game state's current player (i.e., switch players for the game state)
assume best minmax value is a tie

if within MAX_DEPTH threshold:
    for each move left in board of the current game state:
        make the move on the state's board (make sure to use the correct player's piece)
        recur minimax on UPDATED board and incremented depth
        the value returned from minimax recursion above is the new minimax value

        if playing MAX:
            set best minmax value to max of current best minmax value and new minmax value
        if playing MIN: 
            set best minmax value to min of current best minmax value and new minmax value

return best minmax value

Subtle differences in your implementation of the minimax algorithm can lead to completely different results so it is crucial that you follow the algorithm exactly as is written above. Furthermore, note the following:

For our implementation of minimax, player 1 will be MAX and player 2 will be MIN.

MAX_DEPTH should be 5 (already defined as a macro)

At the beginning of your algorithm, assume the best minmax value is a tie

Your Task

Complete the implementation of Tic Tac Toe below. Pay attention to the hints in the code and in the background info.

Download the files below (it’s easiest if you right click and then choose download or save)

tic_tac_toe.h

Contains the declaration of the lab you’ll be implementing. Do not modify any of the given code.

tic_tac_toe.cpp

Contains the definition of the lab you’ll be implementing.

main.cpp

Contains the main program to run your game in the console. Do not edit this file. The main() has already been written for you to enable the AI mode if there’s a command line argument or leave the game as a 2 human player game otherwise.

Read aboutstructs and macros to better understand the code given to you.
Once you have downloaded all the files, inspect them. Ask questions if you have them.
Implement the two constructors and the destructor. Hint: Your constructors will look very similar to one of the constructors from Lab 5! If constructed correctly, your Tic Tac Toe board should print as follows:
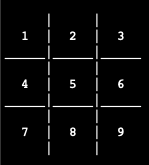
Implement game_status which determines whether the game is over by a win or tie if the game is ongoing.
Run, compile, and test your program by running compiling it and running it in your terminal, while in the directory all these files are located in, and playing the game through several times in human vs human mode. To compile your code, use:
```
 $ g++ -std=c++11 -Wall main.cpp tic_tac_toe.cpp -o ttt
```
BUT if you’re working locally (i.e., VS Code or Visual Studio) on a Windows machine use:
```
 $ g++ -std=c++11 /Wall main.cpp tic_tac_toe.cpp -o ttt
```
This will generate a command line program that takes in one optional command-line argument (CLA). If the program is executed with no CLA, the game will call the constructor with ai_mode as false, which should allow two human players to play together. If there’s a CLA present, the game calls the constructor with ai_mode as true, which should allow a human player to play against your AI (AI will always be player 2).
Implement minimax_algo, the recursive backtracking algorithm as described in the section above, to create your Tic Tac Toe AI.
Run, compile, and test your program by running compiling it and running it in your terminal, while in the directory all these files are located in, and playing the game through several times in human vs AI form. You AI won’t be the smartest but if implemented correctly, it should be smart enough!

Requirements

Your submission will be tested and graded by an autograder, for this reason it cannot be stressed enough that your program must exactly follow the assignment specifications:

You compiles with no warnings or error messages
Your program successfully executes Tic Tac Toe with two human players
Your minimax algorithm produces valid moves
Your minimax algorithm is implemented as stated above and produces the optimal moves

Handing in

To submit your solution to Gradescope, select all of the following files and use the drag and drop option:

tic_tac_toe.h
tic_tac_toe.cpp
main.cpp

Grade Breakdown

You must successfully meet requirements 1 through 4 in order to receive credit for this assignment.

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

Background info by Dr. Marco Alvarez, used and modified with permission.

URI CSC 212

Lab 18