URI CSC 212 logo URI CSC 212

Lab 19

Introduction to Trees

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide you an introduction to trees, which we’ll be seeing a lot of over the next few weeks.

Background Info

Trees

Trees are a Data Structure that models hierarchical data, as opposed to a LinkedList which stores linear data. Trees are a data structure similar to LinkedLists in that we use Nodes to store data and references to other Nodes containing more data. Except where a LinkedList grows left to right and has at most two references (front and back in a Doubly-Linked List) a Tree grows top to down and each Node can have any number of references.

Lets dive into some terminology:

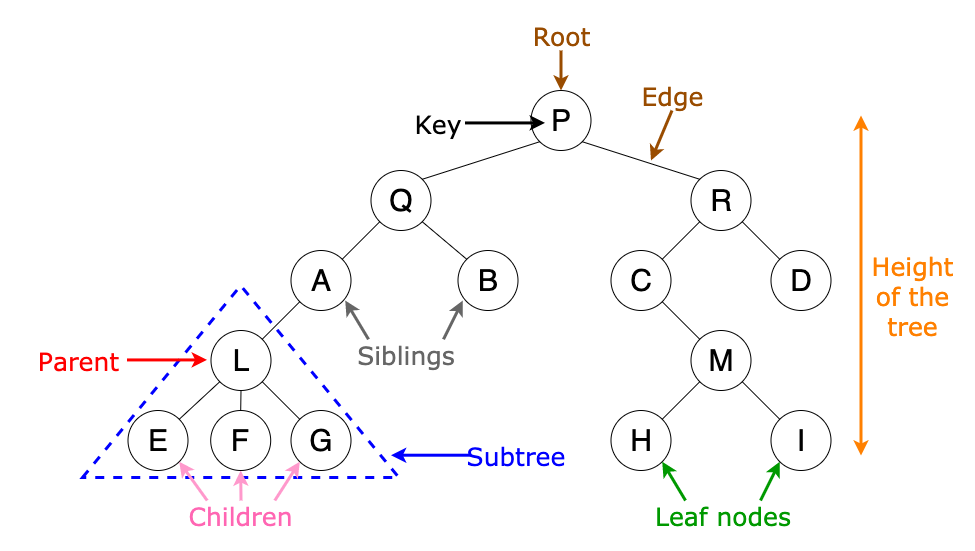
Root
The first Node in the tree. Similar to the Head Node in a LinkedList.
Edge
The connection between Nodes. Typically a pointer.
Parent
Any Node that has a child.
Child
Any Node belonging to a Parent.
Siblings
Any Nodes that share the same parent.
Leaf
Any Node without any children
Subtree
By definition, every Subtree is its own Tree, and must follow the same rules as its Parent.

Tree Data Structures are very flexible, and can be tweaked to fit a problem as needed. Without any bounding rules, a Tree can have any number of children at each Node. Observe:

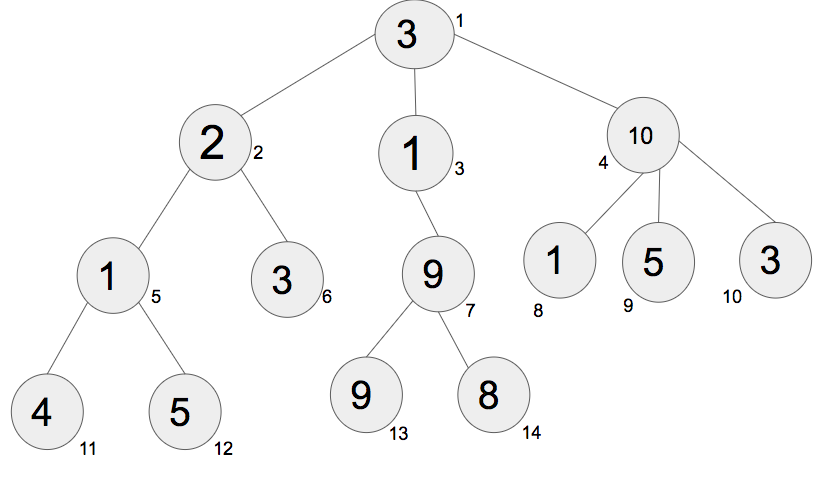
These types of trees are typically known as “K-Ary Trees” and are implemented in slightly more advanced algorithms than we’ll be covering today, so lets simplify things a bit. Behold, the Binary Tree!

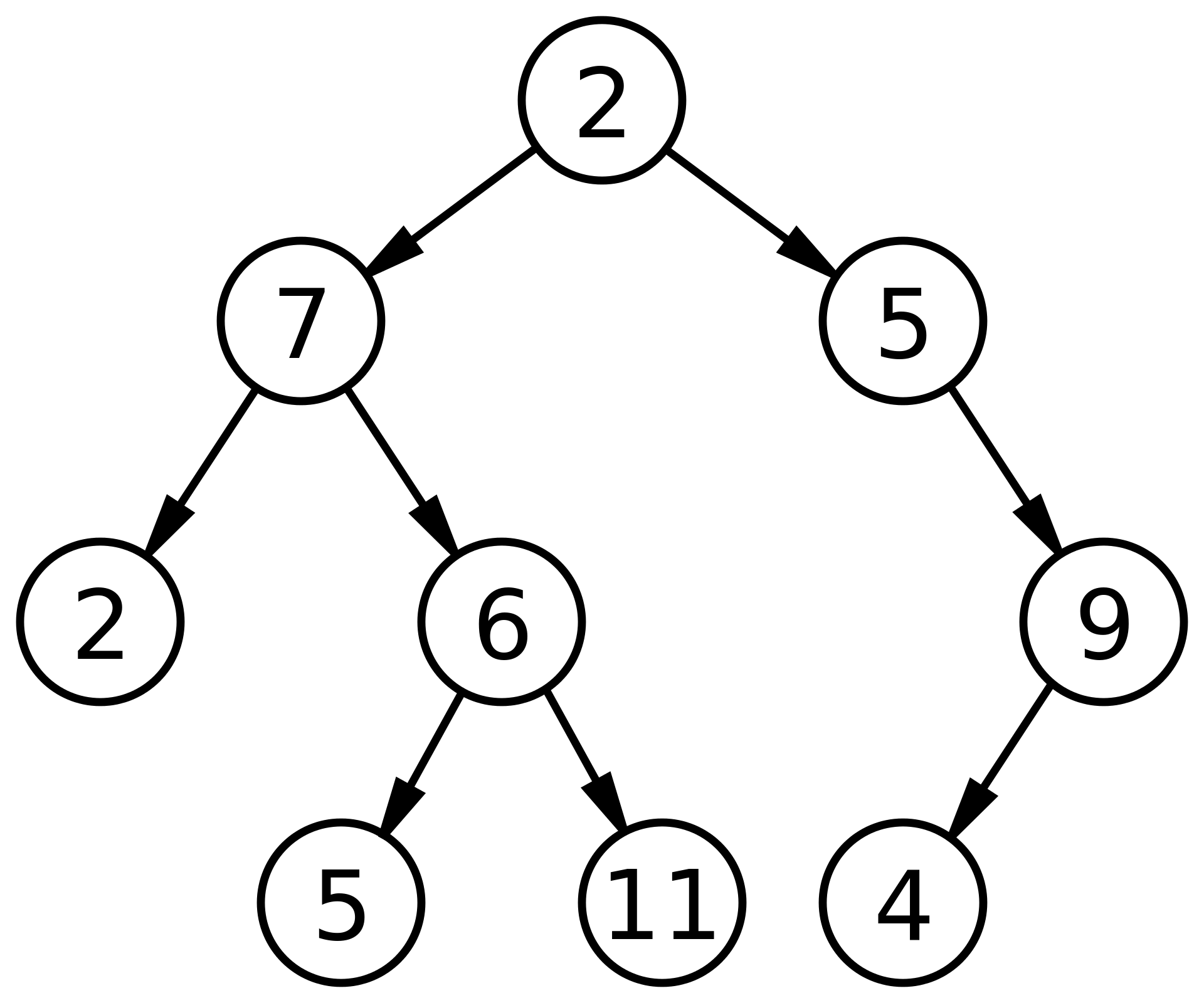
Binary trees have a simple rule:

and are not to be confused with Ternary Trees:

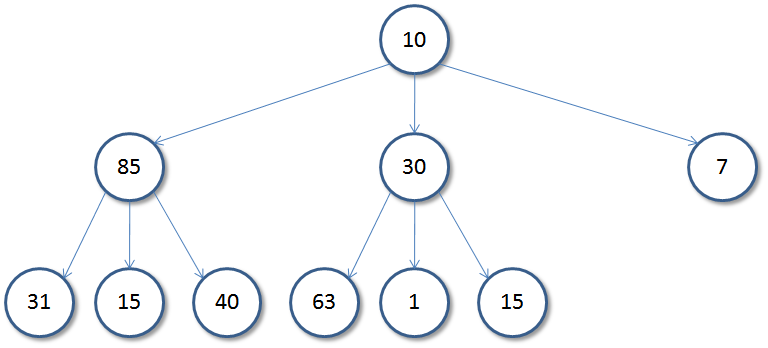
which have the following rule:

For all of the above definitions, Trees can be further classified as Full, Complete, and Balanced or Unbalanced. For all of these definitions, we’ll use a Binary Tree as examples, but be aware that these can be applied to any K-Ary Tree.

Full Trees

A Tree is classified as “Full” if every Node other than the leaves have K children.

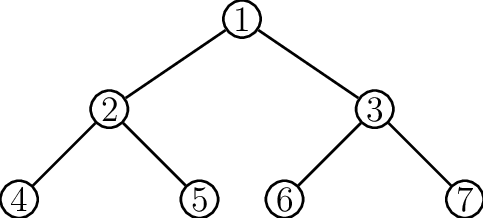
Complete Trees

A Tree is classified as “Complete” if every Node other than the leaves have K children, with an exception for the last row. This last row must have all Leaf Nodes as far left as possible.

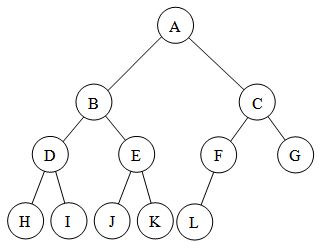
Tree Balance

A Tree is considered balanced if the following is observed:

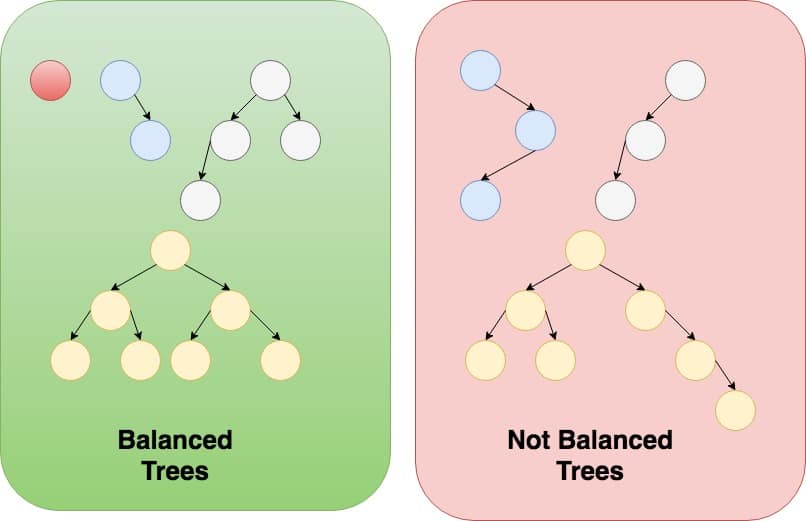
Don’t worry too much about Tree Balance, we’ll cover this in depth at a later date. Just know it exists and is accomplished by rotating subtrees.

Tree Traversal

Unliked a LinkedList, we can traverse a Tree structure in many different ways. Traversal of a tree (like all operations) are done recursively (yaaaaaaay!) Typically, we use a Node* to mark where we currently are and assign it as needed to perform the traversal. Very similar to how we used a ‘curr’ Node in our LinkedList class. Lets re-use one of our Trees from earlier to see how we could display its contents using the three most commonly used traversal methods:

In-Order Traversal
Traverse left
Visit Root
Traverse right

This would yield the output: 4 2 5 1 6 3 7

Pre-Order Traversal
Visit Root
Traverse left
Traverse right

This would yield the output: 1 2 4 5 3 6 7

Post-Order Traversal
Traverse left
Traverse right
Visit Root

This would yield the output: 4 5 2 6 7 3 1

Your Task

Complete the implementation of a binary tree. Pay attention to the hints in the code (CPP AND H FILES).

  1. Download the files below (it’s easiest if you right click and then choose download or save)

    binary_tree.h
    Contains the declaration of the lab you’ll be implementing. Do not alter any of the given function signatures. This time, we’re using a struct for our Node, instead of a class. Read about structs.
    binary_tree.cpp
    Contains the definition of the lab you’ll be implementing.
    test.cpp
    EMPTY TEST FILE (with a template for you to follow). You should add your own test cases to this file.
    doctest.h
    The library we’ll be using for our own automated tester. There’s a ton of code in here so don’t worry too much about understanding everything it does– just know the library is extremely powerful and we’ll only be scratching the surface of everything it can do. Do not edit this file.
  2. Once you have downloaded all the files, inspect them. Ask questions if you have them.
  3. Create your own makefile to compile and run your program. Refer to Lab 3 as needed.
  4. Complete the implementation of insert. Pay attention to the comments and hints in the code (CPP AND H FILES). Refer to the course material (slides, readings, and background info above) as needed.
  5. Add your own test cases for the functions you just completed. For now, you won’t have any “proof” that insert works, beyond not getting a seg fault or an infinite loop.
  6. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. For now, you won’t have any “proof” that insert works, beyond not getting a seg fault or an infinite loop. Debug as needed.
  7. Complete the implementation of search. Pay attention to the comments and hints in the code (CPP AND H FILES). Refer to the course material (slides, readings, and background info above) as needed.
  8. Add your own test cases for the functions you just completed. Use search to test insert, and vice-versa.
  9. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. Debug as needed.
  10. Complete the implementation of display_in_order, display_post_order, and display_pre_order. Pay attention to the comments and hints in the code (CPP AND H FILES). Refer to the course material (slides, readings, and background info above) as needed.
  11. Add your own test cases for the functions you just completed. Now that you have a full implementation, you should be able to test all your functions fully and extensively.
  12. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. Debug as needed.

Requirements

Your submission will be tested and graded by an autograder, for this reason it cannot be stressed enough that your program must exactly follow the assignment specifications:

  1. All binary tree functions work as expected.

Handing in

To submit your solution to Gradescope, select all of the following files and use the drag and drop option:

Grade Breakdown

You must successfully meet requirement 1 in order to receive credit for this assignment.

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

Original assignment by Christian Esteves, used and modified with permission.