Binary Search Trees

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

This lab will help you solidify your understanding of binary search trees.

Background Info

A binary search tree is a data structure to store arbitrary “items” in a way that allows extremely rapid searches, insertion, and removal. They rely on sortable “keys” which are used to store and look up a given node. These “keys” and the way they are stored means that during a lookup, at each step, up to half of the entire tree can be discarded from the search.

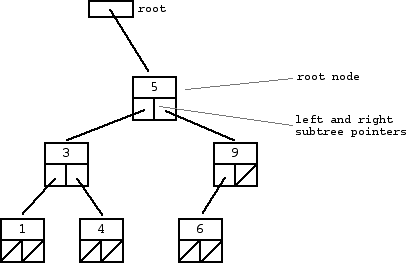
As you can see from the image above, a Binary Search Tree is ordered in the following way:

A root node pointer which always points to the initial value
Each node has a left pointer and a right pointer
- The left pointer points to a node whose key is less than the parent node’s key
- The right pointer points to a node whose key is greater than the parent node’s key
This pattern continues throughout the BST

The resulting tree will have two subtrees stemming from the root node. The left-hand subtree will have key values which are all less than the root node’s key. The right-hand subtree will have key values which are all greater than the root node’s key.

Check out this binary search tree visualization from USFCA.

Your Task

Complete the implementation of a binary search tree. Pay attention to the all the notes below.

Make a copy of your Lab 19 files do not modify the originals.
Rename binary_tree.cpp to bs_tree.cpp. Change your constructor’s and class name (from BinaryTree to BSTree– don’t forget the BinaryTree:: before all the functions too!). Make sure to change the #include from binary_tree.h to bs_tree.h.
Rename binary_tree.h to bs_tree.h. Change your constructor’s and class name (from BinaryTree to BSTree)
Compile your code to make sure 1-3 were done correctly. Update anything you missed.
In bs_tree.h:
- a) Add a public function called height(). This function should take no parameters and should return an integer representing the height of the tree.
- b) Add a private function called height(). This function should take in a Node* and should return an integer representing the height of the tree.
- c) Remove parent_data from both insert() functions. Update the private insert() so it returns a Node* instead of a bool.
- d) Update your public search() function. This function should take in an integer to search for and should return a boolean representing whether the data was found in the tree or not.
- e) Update your private search() function. This function should take in an integer to search for and a Node* to traverse the tree and should return a boolean representing whether the data was found in the tree or not.
- f) Add a private function called destroy(). This function should take in a Node* as a parameter and should return void.
Update bs_tree.cpp so it matches bs_tree.h. Namely:
- a) Add a public function called height(). This function should take no parameters and should return an integer representing the height of the tree.
  - Like the relationship between the rest of the public and private functions, this function should call the private method on the root, and return the resulting integer representing the height of the tree.
- b) Add a private function called height(). This function should take in a Node* and should return an integer representing the height of the tree.
  - The private method should recursively traverse the tree to return an integer representing the height of the subtree rooted at the node passed in.
    
    Note: Calling the height method on an empty tree should return -1 as a tree with one node is of height 0. The -1 is used to distinguish between the two.
- c) Remove parent_data from both insert() functions. Update the private insert() so it returns a Node* instead of a bool.
  - Update the public function per the private function’s new signature. When you call the private function, set the tree’s root to whatever the private call returns.
  - Update the private function so that it matches its new signature.
  - Update the private function so that it inserts the node in the correct place in the tree, per BST ordering. Assume duplicate keys will not be inserted.
- d) Update your public search() function. This function should take in an integer to search for and should return a boolean representing whether the data was found in the tree or not.
  - Like the relationship between the rest of the public and private functions, this function should call the private method on the root, and return the resulting boolean.
- e) Update your private search() function. This function should take in an integer to search for and a Node* to traverse the tree and should return a boolean representing whether the data was found in the tree or not.
  - Recall BST ordering when rewriting this function!
- f) Add a private function called destroy(). This function should take in a Node* as a parameter and should return void.
  - This function should destroy the entire subtree starting at node passed in, recursively. Make sure that you only delete your current node after all subtrees have been freed (otherwise you’ll have a memory leak!). HINT: Think about which type of traversal would be best to implement this method. It’ll look very similar to one of your display functions, except that instead of printing, you’ll be deleting the node (so if your parameter is called curr, you’d do delete curr).
Create a tree destructor (destructors are named with a ~ and then the class name, so in this case ~BSTree) in bs_tree.cpp so that it calls destroy() on the root of the tree. Make sure to add the destructor declaration to your header file as well!)
Update test.cpp to test all of your public functions correctly. Make sure to change the #include from binary_tree.h to bs_tree.h
Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. Debug as needed.
Define and implement the following functions into your BSTree class:
- isComplete(), public function that takes in no parameters and returns a boolean. Tells us if the tree is complete or not.
- isFull(), public function that takes in no parameters and returns a boolean. Tells us if the tree is full or not.
- isComplete(), private function that takes in a Node* to traverse the tree, an int index to determine its position, and an int count telling us how many nodes are in the tree, and returns a boolean. Tells us if the tree is complete or not.
  - HINT: There is a relationship between how far down the tree you are and the # of total nodes in the tree to determine completeness.
- isFull(), private function that takes in a Node* to traverse the tree and returns a boolean. Tells us if the tree is full or not.
- size(), private function that takes in a Node* to traverse the tree and returns an int count telling us how many nodes are in the tree.
Update test.cpp to test the public isComplete() and isFull() functions.

Requirements

Your submission will be tested and graded by an autograder, for this reason it cannot be stressed enough that your program must exactly follow the assignment specifications:

All binary search tree functions work as expected.

Handing in

To submit your solution to Gradescope, select all of the following files and use the drag and drop option:

bs_tree.h
bs_tree.cpp
test.cpp

Grade Breakdown

You must successfully meet requirement 1 in order to receive credit for this assignment.

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

Original assignment by Dr. Marco Alvarez, modified assignment version by Christian Esteves, used and modified (again) with permission.

URI CSC 212

Lab 20