URI CSC 212 logo URI CSC 212

Lab 22

Graphs, BFS, & DFS

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide background on Graphs, Breadth-First Search (DFS), and Depth-First Search (DFS.

Background Info

Graphs

Graphs are non-linear data structures made of Nodes, where each Node is connected to any number of other Nodes in the Graph. The connections between Nodes are called Edges. Graphs have two main properties that determine how you are allowed to traverse/utilize them: directed, undirected, weighted, and unweighted. Modeling our data in this form allows us to perform tasks such as path finding.

Directed Unweighted Graphs

In a Directed Unweighted Graph, you are limited in the direction you can traverse along the Graph (you can go to 1 from 0, but not to 0 from 1), and all steps have the same cost (if any.)

Directed Weighted

In a Directed Weighted Graph, you are still limited in the direction you can traverse along the Graph (you can go to 1 from 0, but not to 0 from 1), and each step has a different cost.

Undirected Unweighted Graphs

In an Undirected Unweighted Graph, you are NOT limited in the direction you can travel along the Graph (you can go to 1 from 0, AND from 0 from 1), and all steps have the same cost (if any.)

Undirected Weighted Graphs

In an Undirected Weighted Graph, you are NOT limited in the direction you can travel along the Graph (you can go to 1 from 0, AND from 0 from 1), and each step has a different cost. This is the type of Graph we’ll be covering today.

Graph Representation

Graph have 3 main methods of being represented: Adjacency List, Adjacency Matrix, and Incidence Matrix. Let’s take a look at each of these.

Adjacency List

In an Adjacency List, we use a collection of lists to represent the graph. Each list represents a vertex, while the contents of those lists represent connections to other vertices. In the case of a weighted graph, the weights are also stored. This is the main focus of today’s lab. The Undirected Weighted Graph from above would be represented as such:

Adjacency Matrix

In an Adjacency Matrix, we use a matrix of integers to represent the graph. The X coordinate represents the source, while the Y coordinate represents the destination. The value at that cell is the weight of that edge. The Undirected Weighted Graph from above would be represented as such:

  0 1 2 3 4 5
0 0 7 9 0 0 14
1 7 0 10 15 0 0
2 9 10 0 11 0 2
3 0 15 11 0 6 0
4 0 0 0 6 0 9
5 14 0 2 0 9 0
Incidence Matrix

In an Incidence Matrix, we use a matrix of Booleans to represent the graph. The X coordinate represents the source, while the Y coordinate represents the destination. A the value at that cell is the incidence relation represents whether those two Vertices are incident (connected, in this context.) The Undirected Weighted Graph from above would be represented as such:

  0 1 2 3 4 5
0 0 1 1 0 0 1
1 1 0 1 1 0 0
2 1 1 0 1 0 1
3 0 1 1 0 1 0
4 0 0 0 1 0 1
5 1 0 1 0 1 0

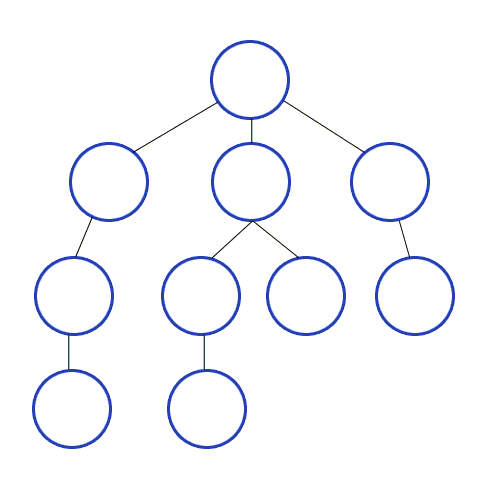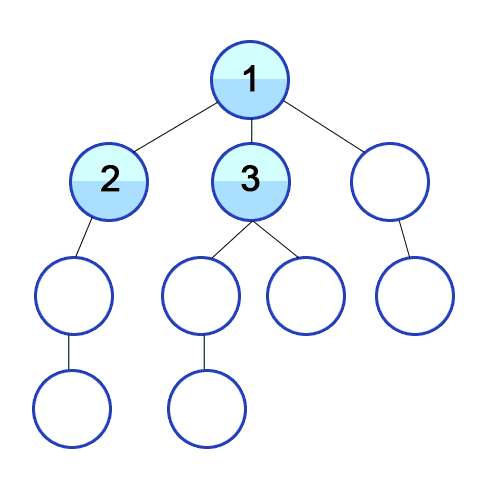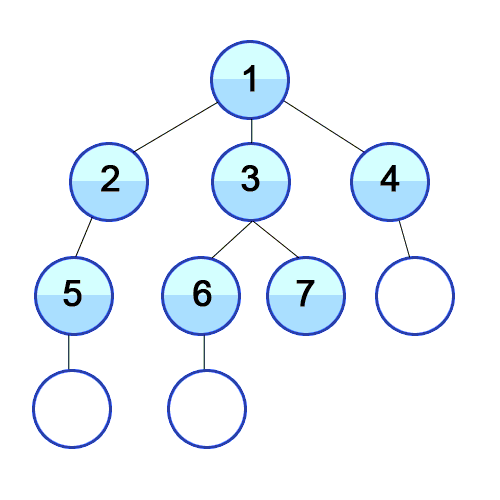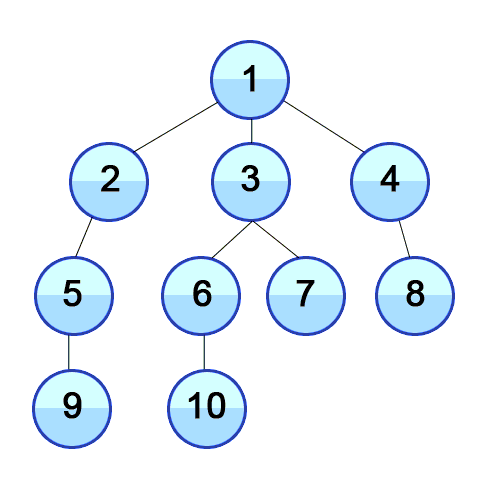
In BFS we travel as wide as we can, using a Queue to mark the current Vertex’s children to keep the order to visit them. For the following animation, here are the first few steps:

Why care about BFS? BFS is used to find the shortest path between two points (in unweighted undirected graphs, such as getting cellphone data from the closest cell tower), when buying flights to determine possible itineraries, finding relatives via DNA-sites (i.e., ancestry.com), web crawlers, and more!

In DFS we travel as deep down a path as we can, and upon hitting a dead end we backtrack as far as we need to hit another path. This process then repeats.

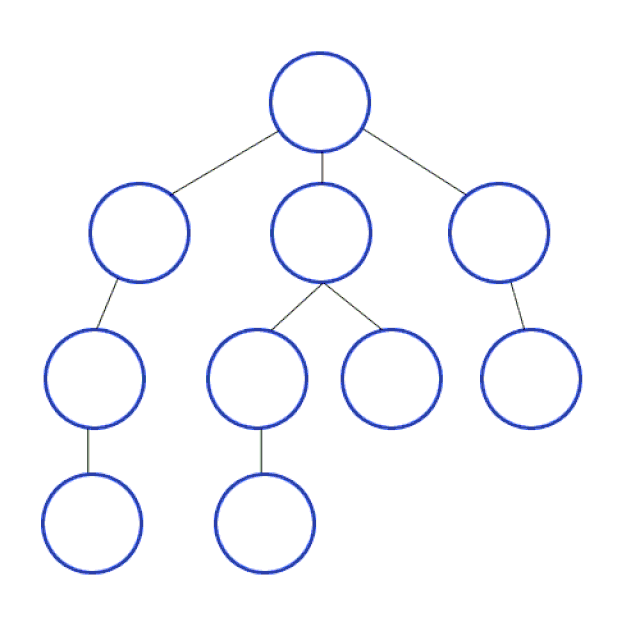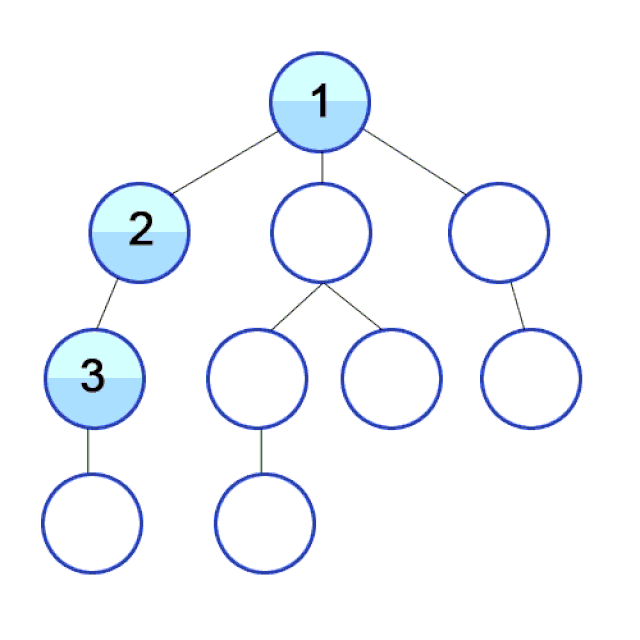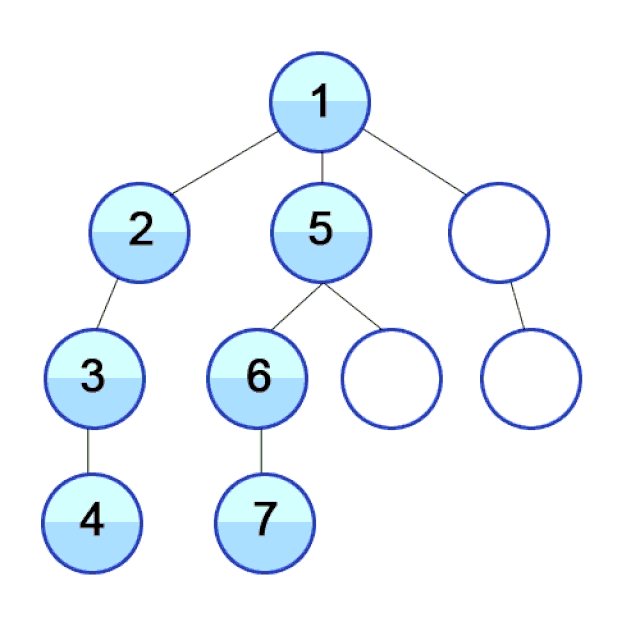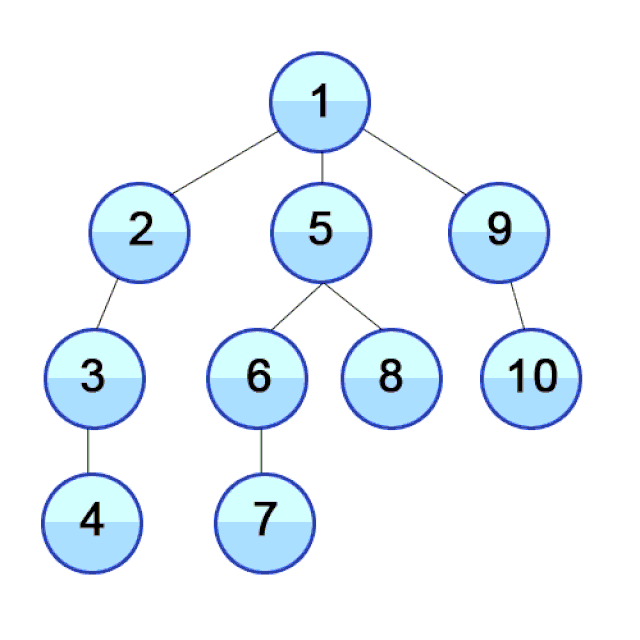
Why care about DFS? DFS is used to find the shortest path between two points (in weighted directed graphs, such as finding the fastest path to a location in traffic), solving mazes, web crawlers, robots that clean your floor, and more!

Your Task

Complete the implementation of an undirected weighted graph. Pay attention to the hints in the code (CPP AND H FILES).

  1. Download the files below (it’s easiest if you right click and then choose download or save)

    graph.h
    Contains the declaration of the lab you’ll be implementing. Do not alter any of the given function signatures.
    graph.cpp
    Contains the definition of the lab you’ll be implementing.
    test.cpp
    EMPTY TEST FILE (with a template for you to follow). You should add your own test cases to this file.
    doctest.h
    The library we’ll be using for our own automated tester. There’s a ton of code in here so don’t worry too much about understanding everything it does– just know the library is extremely powerful and we’ll only be scratching the surface of everything it can do. Do not edit this file.
  2. Once you have downloaded all the files, inspect them. Ask questions if you have them.
  3. Create your own makefile to compile and run your program. Refer to Lab 3 as needed.
  4. Complete the implementation of the adjacency list by completing the implementation of ensureValidGraph() and addEdge(). Pay attention to the comments and hints in the code (CPP AND H FILES). Refer to the course material (slides, readings, and background info above) as needed.
    • For a more in-depth explanation of how ensureValidGraph() and addEdge() work, watch this video (it’s from last semester so the lab numbers are off but the task is the same).
  5. Add your own test cases for the functions you just completed. Now that you have a full implementation, you should be able to test all your functions fully and extensively.
  6. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. Debug as needed.
  7. Complete the implementation of BFS. Pay attention to the comments and hints in the code (CPP AND H FILES). Refer to the course material (slides, readings, and background info above) as needed.
  8. Add your own test cases for the functions you just completed. Now that you have a full implementation, you should be able to test all your functions fully and extensively.
  9. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. Debug as needed.
  10. Complete the implementation of DFS. Pay attention to the comments and hints in the code (CPP AND H FILES). Refer to the course material (slides, readings, and background info above) as needed.
  11. Add your own test cases for the functions you just completed. Now that you have a full implementation, you should be able to test all your functions fully and extensively.
  12. Run, compile, and test your program by running make in your terminal, while in the directory all these files are located in. Debug as needed.

Requirements

Your submission will be tested and graded by an autograder, for this reason it cannot be stressed enough that your program must exactly follow the assignment specifications:

  1. All graph functions work as expected.

Handing in

To submit your solution to Gradescope, select all of the following files and use the drag and drop option:

Grade Breakdown

You must successfully meet requirement 1 in order to receive credit for this assignment.

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

Original assignment by Christian Esteves, used and modified with permission.