On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide some insight into advanced recursive algorithms. Being comfortable with reading, writing, and analyzing recursive algorithms is crucial for understanding all our upcoming topics.

---

Background Info

Fractals are geometric figures in which each part has the same statistical character as the entire figure. In other words, the same patterns repeated at varying scales. Here are a few! Can you find the repeating patterns in each of these fractals?

Sierpinski Carpet

Sierpinski Carpet: A square with 8 smaller squares one-third its size placed around it.

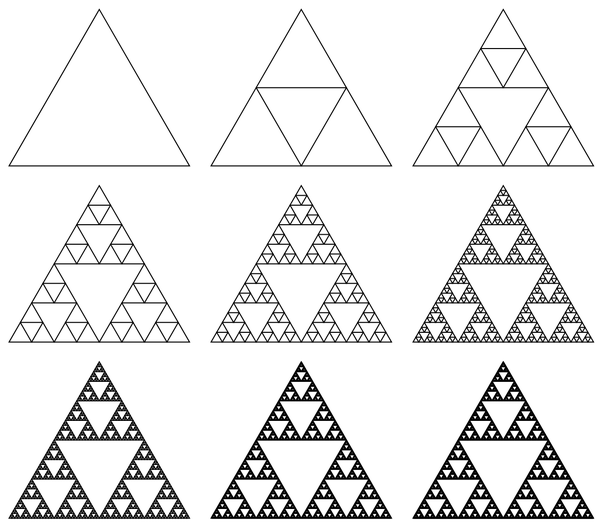
Sierpinski Triangle

Sierpinski Triangle: An equilateral triangle subdivided into 4 smaller equilateral triangles, with the inner triangle removed.

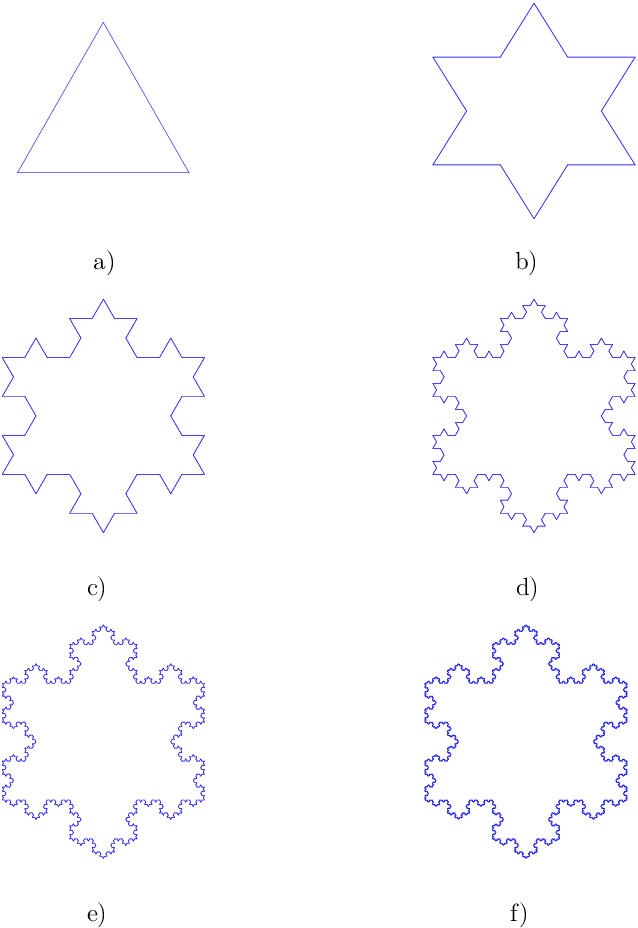
Koch Snowflake

Koch Snowflake: An equilateral triangle where each edge gets a triangle placed one-third the size of the original, and has its base removed.

Now that we understand the pattern, we need to learn how to implement them! To this effect, we will be utilizing ‘L-systems’.

---

Lindenmayer Systems (L-Systems)

An ‘L-system’ is an alphabet of symbols that form strings, which represent a collection of production rules. In this case, we will be the following ‘L-system’:

F : Move forward

- : Turn left by some degree

+ : Turn right by some degree

So, a valid string for this system could be

Draw out the shape generated by the following strings using our system:

1. “F + F + F + F”, run with a turn degree of 90
2. “F - F - F”, run with a turn degree of 60

---

Your Task

You will implement two of the fractal shapes above by utilizing an ‘L-system’. Your task is to create recursive functions that generate the string necessary to draw the shape, for a Sierpinski Triangle and a Koch Snowflake. You have been supplied with some skeleton code to get you started, as well as a python script to convert a generated string into a .png image representation.

Here are some animations to help you in determining the rules for your strings:

Sierpinski Triangle

Koch Snowflake

To understand how the Koch Snowflake is drawn, these images show the completion of the image at the 3 loop iterations in the koch_snowflake function.

After the first iteration:

After the second iteration:

After the third iteration:

Notes

• Get a feeling for the string you should be generating BEFORE you start coding.
• You may code your solutions on this repl.it page.
  • When you run your code, the python script will be run automatically on your outputted string!
• Utilize this website to see your L-System drawn slowly.
• To use the python file locally: python3 l-system-plotter.py l-system.txt <output file name> <degree for turns>
  • If you’re not using the repl.it, you can download and use the python script locally.
  • The degree argument should be 60 for both of these problems!

---

Requirements

1. Outline an algorithm to create an L-System for the Koch Snowflake.
2. Outline an algorithm to create an L-System for the Sierpinski Triangle
3. Complete the function to produce a Koch Snowflake
4. Complete the function to produce a Sierpinski Triangle

---

Handing in

Please call a TA over to get checked off before leaving your lab section (regardless of how far you got). If you want to continue working on your lab after your lab section, come to hours to get checked off.

---

Grade Breakdown

This assignment covers advanced recursion and your level of knowledge on them will be assessed as follows:

• To demonstrate an awareness of these topics, you must:
  • Successfully meet requirement 1 and 2
• To demonstrate an understanding of these topics, you must:
  • Successfully meet requirements 1, 2 and (3 or 4)
• To demonstrate competence of these topics, you must:
  • Successfully meet requirements 1 through 4

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

---

Original assignment by Dr. Marco Alvarez, used and modified with permission.