On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide you an introduction to trees, which we’ll be seeing a lot of over the next few weeks.

---

Background Info

Trees

Trees are a Data Structure that models hierarchical data, as opposed to a LinkedList which stores linear data. Trees are a data structure similar to LinkedLists in that we use Nodes to store data and references to other Nodes containing more data. Except where a LinkedList grows left to right and has at most two references (front and back in a Doubly-Linked List) a Tree grows top to down and each Node can have any number of references.

Lets dive into some terminology:

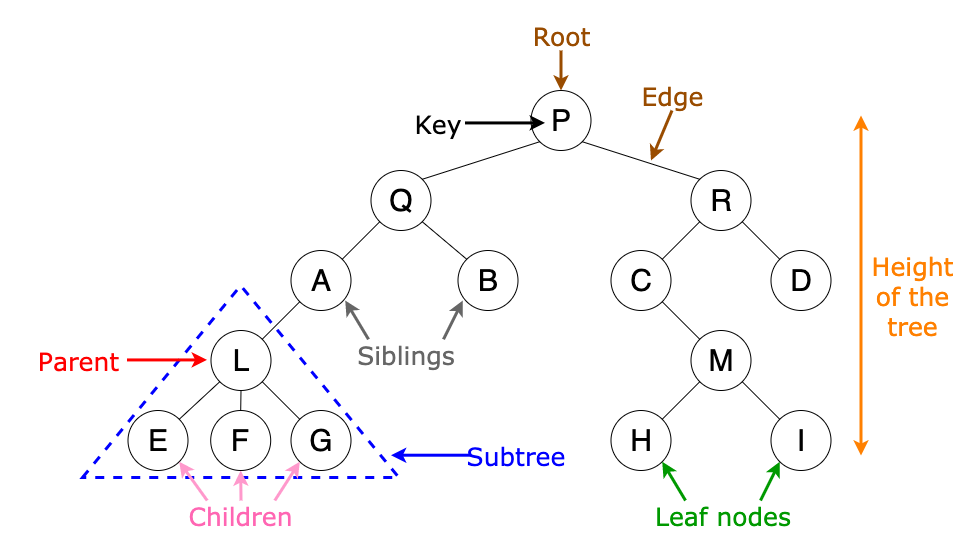
Root

The first Node in the tree. Similar to the Head Node in a LinkedList.

Edge

The connection between Nodes. Typically a pointer.

Parent

Any Node that has a child.

Child

Any Node belonging to a Parent.

Siblings

Any Nodes that share the same parent.

Leaf

Any Node without any children

Subtree

By definition, every Subtree is its own Tree, and must follow the same rules as its Parent.

Tree Data Structures are very flexible, and can be tweaked to fit a problem as needed. Without any bounding rules, a Tree can have any number of children at each Node. Observe:

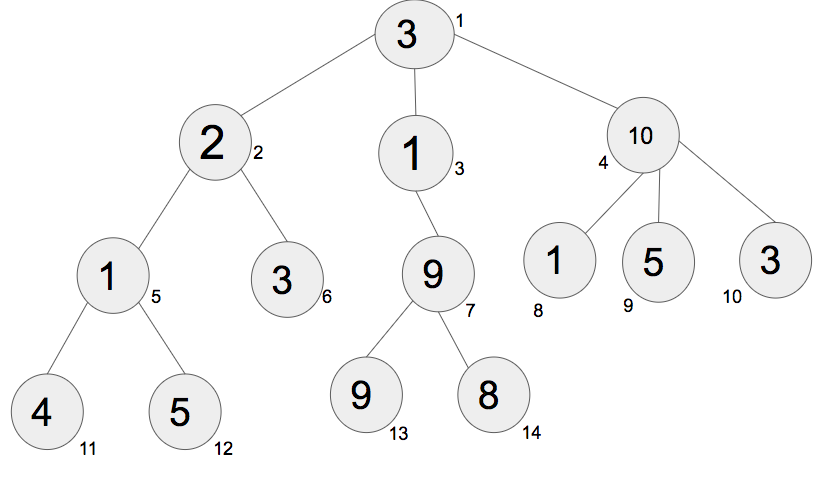
These types of trees are typically known as “K-Ary Trees” and are implemented in slightly more advanced algorithms than we’ll be covering today, so lets simplify things a bit. Behold, the Binary Tree!

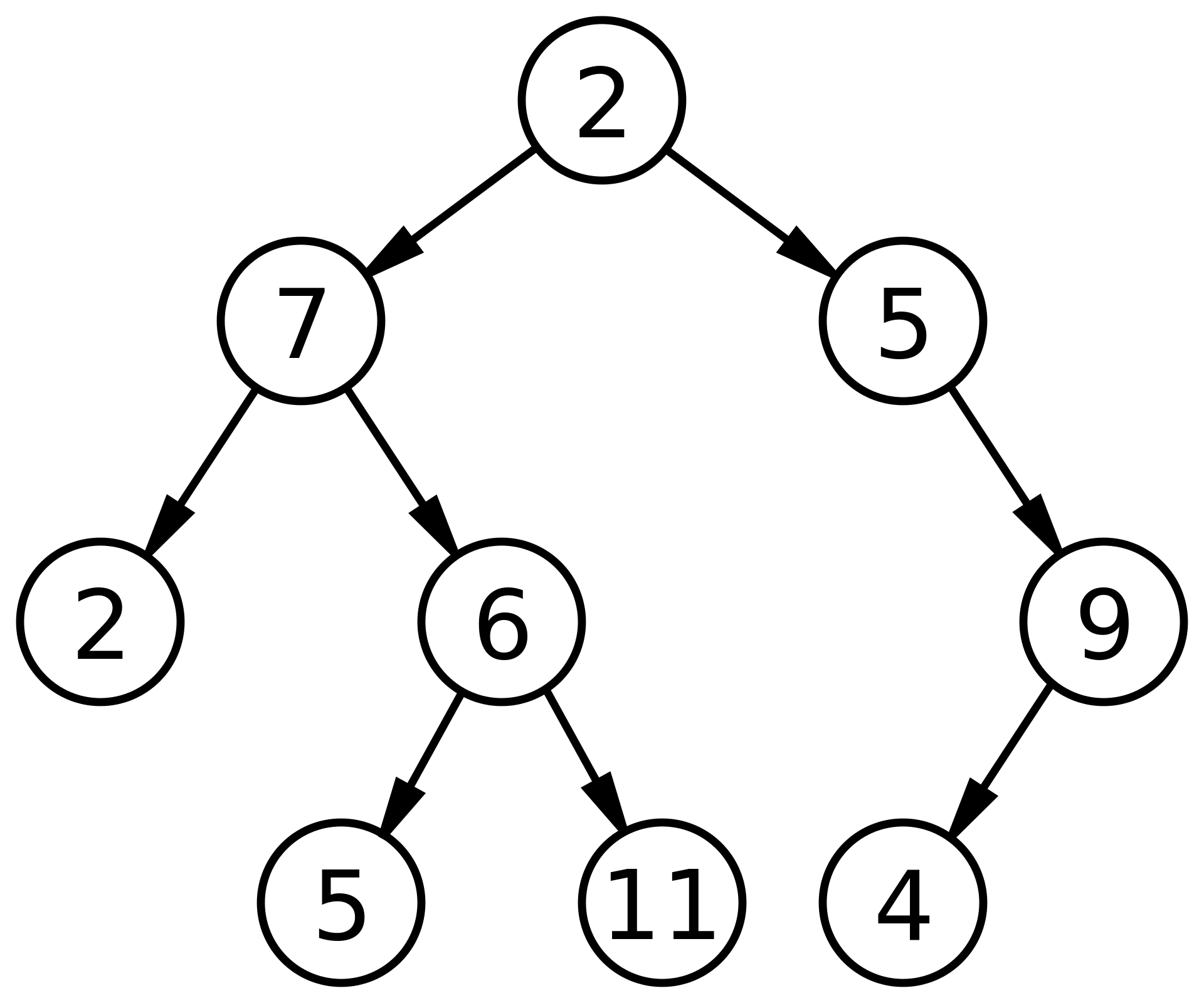
Binary trees have a simple rule:

• Each Node has at most 2 children.

and are not to be confused with Ternary Trees:

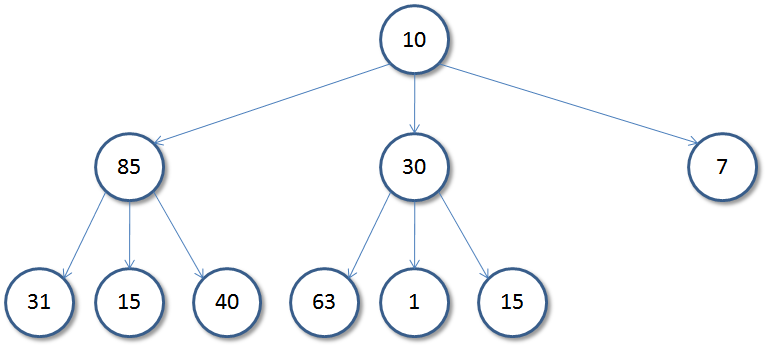
which have the following rule:

• Each Node has at most 3 children.

For all of the above definitions, Trees can be further classified as Full, Complete, and Balanced or Unbalanced. For all of these definitions, we’ll use a Binary Tree as examples, but be aware that these can be applied to any K-Ary Tree.

Full Trees

A Tree is classified as “Full” if every Node other than the leaves have K children.

Complete Trees

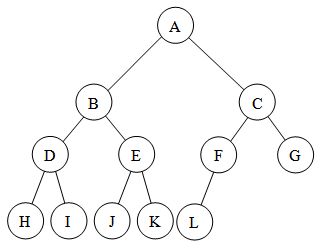
A Tree is classified as “Complete” if every Node other than the leaves have K children, with an exception for the last row. This last row must have all Leaf Nodes as far left as possible.

Tree Balance

A Tree is considered balanced if the following is observed:

• Each sub-tree is balanced and the height of the two sub-trees differ at most by 1.

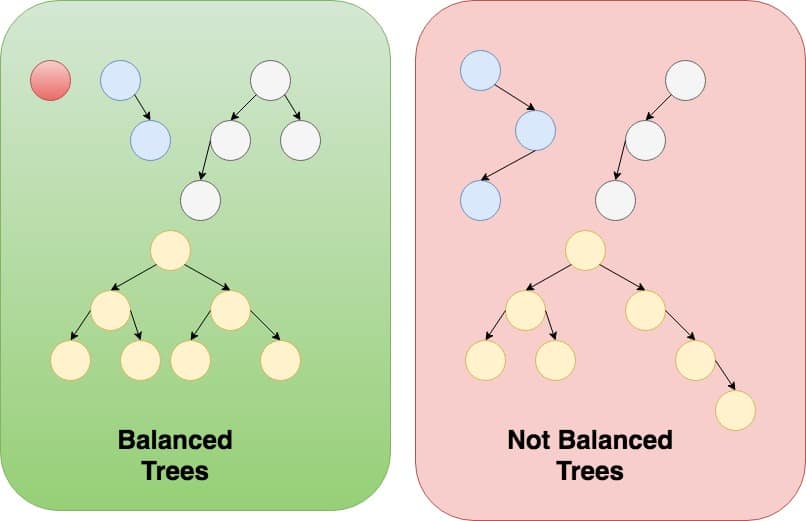
Don’t worry too much about Tree Balance, we’ll cover this in depth at a later date. Just know it exists and is accomplished by rotating subtrees.

Tree Traversal

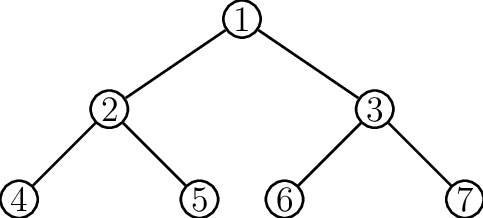
Unliked a LinkedList, we can traverse a Tree structure in many different ways. Traversal of a tree (like all operations) are done recursively (yaaaaaaay!) Typically, we use a Node* to mark where we currently are and assign it as needed to perform the traversal. Very similar to how we used a ‘curr’ Node in our LinkedList class. Lets re-use one of our Trees from earlier to see how we could display its contents using the three most commonly used traversal methods:

In-Order Traversal

Traverse left
Visit Root
Traverse right

This would yield the output: 4 2 5 1 6 3 7

Pre-Order Traversal

Visit Root
Traverse left
Traverse right

This would yield the output: 1 2 4 5 3 6 7

Post-Order Traversal

Traverse left
Traverse right
Visit Root

This would yield the output: 4 5 2 6 7 3 1

---

Your Task

Create your own solution, from scratch, to complete the requirements listed below.

---

Requirements

1. Create the following Trees on paper/MS Paint/etc. (the values are yours to decide) and display their contents using all three traversal methods:

   1. Full Binary Tree with 7 Nodes
   2. Complete Ternary Tree with 8 Nodes
   3. Balanced 4-ary Tree with 15 Nodes

2. Implement and test a simple Binary Tree. Use the following function definitions to help you:

   // Search the Tree for the Node containing 'parent_data' and append a new Node containing
   // 'new_data'. Prefer appending to the Left.
   void insert(int parent_data, int new_data);
      
   // Search the Tree for a Node containing 'data'. Returns 'true' if it exists, 'false' otherwise.
   bool search(int data);
      
   // Display the tree according to the rules for each traversal method outlined above.
   void display_in_order();
   void display_post_order();
   void display_pre_order();
      
   // HINT: For all functions, you'll need a helper function that also accepts a Node* as an argument to traverse the tree!
   

3. Do a quick search on different types of trees and choose one to answer the following questions on it:

   1. What type of tree is it?
   2. What are its properties and use cases?
   3. What makes is special/unique from other trees (think: what makes it good at what it’s used for)?
   4. Briefly (3-5 sentences) describe how you think you’d modify your insert() function (from req #2) for this specific type of tree (it doesn’t have to be 100% correct, we just want you put some good thought into it).

---

Handing in

Please call a TA over to get checked off before leaving your lab section (regardless of how far you got). If you want to continue working on your lab after your lab section, come to hours to get checked off.

---

Grade Breakdown

This assignment covers the topic of introduction to trees and your level of knowledge on it will be assessed as follows:

• To demonstrate an awareness of these topics, you must:
  • Successfully meet requirement 1
• To demonstrate an understanding of these topics, you must:
  • Successfully meet requirements 1 and 2
• To demonstrate competence of these topics, you must:
  • Successfully meet requirements 1 through 3

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.