On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide background on Heaps.

---

Background Info

Heaps

Heaps are special implementations of Complete Binary Treess and come in two flavors: Min-Heap and Max-Heap.

Min-Heap (left) and Max-Heap (right)

The difference between these structures are their special rules:

Min-Heap

The key at the root node must be the minimum among the keys present in its children.

Max-Heap

The key at the root node must be the maximum among the keys present in its children.

Heap Operations

For most operations in a Heap, we need to envision each Node in a heap as being “indexed” (not literally indexed as an array is!) as so:

Heap Notations

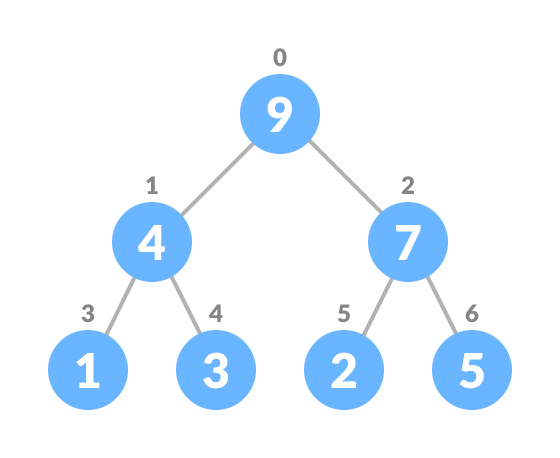
The root Node is index 0. We then we proceed left-right, top-down to “index” the remaining Nodes.

Heapify

Due to the way most Heap operations work, it requires having a “fixer” function that ensures the properties of the Heap are maintained after each operation that could jeopardize them. As usual for Trees, we will be doing so recursively. The basic exercise is:

1. Check if there is a left child

   • Swap the current Node & the Node to its left, if needed.

   • Recursively continue down the left branch.

2. Check if there is a right child

   • Swap the current Node & the Node to its right, if needed.

   • Recursively continue down the left branch.

The end result of the Heapify function is a Tree in which the Min-Heap or Max-Heap property is maintained.

Find Last Element

A common operation is locating the last element in the Heap. Referencing (once again) the “indexing” strategy above, we need an algorithm to locate the right-most element in the bottom-most row of the tree. For our purposes, whenever we find that Node we also want to remove it from the Tree. We can use this algorithm:

1. If we reach nullptr or calculate an index >= the # of Nodes we have in the tree
   • Return nullptr
2. If we’ve located the last element in the tree
   • Return it, mark it to be removed from the Tree
3. Search left, calculating the index for that Node
   • Handle removing the Node if necessary
4. Search right, calculating the index for that Node
   • Handle removing the Node if necessary

Insert

For Insert, we need to ensure that the value being inserted goes into the correct spot in the tree. As a Heap is a Complete Tree, the values are inserted in the order pursuant to the “indexing” strategy shown above. The strategy for this:

1. If we arrive at nullptr, return a new Node object
2. Compare the data being inserted to the data at the current Node
   • Swap the value being inserted with the value at the current Node if needed.
3. If this subtree is a Full Tree with equal sized subtrees, or its left subtree is not a Full Tree
   • Insert to the left
4. Else
   • Insert to the right

Remove Min/Max

Removing the Min/Max of the Heap (depending on the type of Heap) is a fairly common operation. Here’s how we do it:

1. Find the last Node in the tree
2. Swap it with the Min/Max Node
3. Delete the last Node in the tree
4. Heapify!

Delete

Another common operation, and its very similar to Remove Min/max!

1. Find the Node containing the data we wish to remove
2. Find the last Node in the tree
3. Swap it with the Node containing our target data
4. Delete the last Node in the tree
5. Heapify!

---

Your Task

Similar to last week’s lab, we give you a makefile, a unit test file, a doctest header file and a header file with class definitions for HeapNode and HeapTree classes (plus a couple other things). We have supplied heap.cpp to house your class definitions, and test.cpp will serve as your main file.

• heap.h
• heap.cpp
• test.cpp
• doctest.h
• makefile

Thus you will need to follow the specifications in the next section very closely in order to complete the lab correctly.

The HeapNode Header

If you take a look into heap.h, you will notice that it has been pre-written for you. It also contains some code you’ve likely never seen before, like the following:

#ifndef MAX
#define MAX(a,b) ((a > b) ? a : b)
#endif

Similarly to the preprocessor directive defining NULL, this statement defines a macro which actually takes arguments. This allows the preprocessor to replace any instance of MAX(a,b) with ((a > b) ? a : b), which is just a convenient way of getting the max of two numbers, a and b, without even needing to create a function.

All that remains then is the class definitions. For the sake of completeness, HeapNode is the class which will be used for each node of the tree, and HeapTree is the class for the tree itself. What you actually need to do with these classes will be explained in the next section.

The Makefile

While you don’t necessarily need to know how it works, this file is what you will use for both compiling and running your code. The nice thing about a makefile is that if it is created correctly, all you need to do to compile your code is run the command make, no arguments needed. While this is the typical, most basic usage of a makefile, the makefile you are given goes one step further and runs your program immediately after compiling and then removes the binary it created.

Again, all you need to do is run make.

However, do be aware that until you have filled in your header file properly, your program will fail to compile and run. You should only concern yourself with trying to compile the program after implementing the contents of your header. Once you do, your program will compile, but it will still fail all of the tests. This is the point at which you should move on to implementing the methods.

The Unit Tests

The unit tests for this lab, found in test.cpp will perform various tests on each of your method implementations, giving you some feedback if a test fails. You shouldn’t need to do anything with this file, but you’re welcome to create additional test cases.

The Doctest Header

Don’t worry about doctest.h; for our purposes, it is magic.

---

Requirements

Your goal for this lab is to complete the following tasks in order:

1. Diagram the following operations for a min heap:
   • insert: 5, 3, 7, 2 , 4, 6, 8
   • remove_min
   • delete: 4
2. Implement ‘min_heapify()’, ‘find_last()’, ‘remove_min()’, and ‘delete_element()’
3. Copy your entire solution to a new Directory, and modify everything to create a max_heap
   • You will need to re-do the test cases in test.cpp!

---

Handing in

Please call a TA over to get checked off before leaving your lab section (regardless of how far you got). If you want to continue working on your lab after your lab section, come to hours to get checked off.

---

Grade Breakdown

This assignment covers heaps and balanced trees and your level of knowledge on them will be assessed as follows:

• To demonstrate an awareness of these topics, you must:
  • Successfully meet requirements 1
• To demonstrate an understanding of these topics, you must:
  • Successfully meet requirements 1 and 2
• To demonstrate competence of these topics, you must:
  • Successfully meet requirements 1 through 3

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

---