URI CSC 212 logo URI CSC 212

Lab 12

Graphs, BFS, & DFS

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide background on Graphs, Breadth-First Search (DFS), and Depth-First Search (DFS.

Background Info

Graphs

Graphs are non-linear data structures made of Nodes, where each Node is connected to any number of other Nodes in the Graph. The connections between Nodes are called Edges. Graphs have two main properties that determine how you are allowed to traverse/utilize them: directed, undirected, weighted, and unweighted. Modeling our data in this form allows us to perform tasks such as path finding.

Directed Unweighted Graphs

In a Directed Unweighted Graph, you are limited in the direction you can traverse along the Graph (you can go to 1 from 0, but not to 0 from 1), and all steps have the same cost (if any.)

Directed Weighted

In a Directed Weighted Graph, you are still limited in the direction you can traverse along the Graph (you can go to 1 from 0, but not to 0 from 1), and each step has a different cost.

Undirected Unweighted Graphs

In an Undirected Unweighted Graph, you are NOT limited in the direction you can travel along the Graph (you can go to 1 from 0, AND from 0 from 1), and all steps have the same cost (if any.)

Undirected Weighted Graphs

In an Undirected Weighted Graph, you are NOT limited in the direction you can travel along the Graph (you can go to 1 from 0, AND from 0 from 1), and each step has a different cost. This is the type of Graph we’ll be covering today.

Graph Representation

Graph have 3 main methods of being represented: Adjacency List, Adjacency Matrix, and Incidence Matrix. Let’s take a look at each of these.

Adjacency List

In an Adjacency List, we use a collection of lists to represent the graph. Each list represents a vertex, while the contents of those lists represent connections to other vertices. In the case of a weighted graph, the weights are also stored. This is the main focus of today’s lab. The Undirected Weighted Graph from above would be represented as such:

Adjacency Matrix

In an Adjacency Matrix, we use a matrix of integers to represent the graph. The X coordinate represents the source, while the Y coordinate represents the destination. The value at that cell is the weight of that edge. The Undirected Weighted Graph from above would be represented as such:

  0 1 2 3 4 5
0 0 7 9 0 0 14
1 7 0 10 15 0 0
2 9 10 0 11 0 2
3 0 15 11 0 6 0
4 0 0 0 6 0 9
5 14 0 2 0 9 0
Incidence Matrix

In an Incidence Matrix, we use a matrix of Booleans to represent the graph. The X coordinate represents the source, while the Y coordinate represents the destination. A the value at that cell is the incidence relation represents whether those two Vertices are incident (connected, in this context.) The Undirected Weighted Graph from above would be represented as such:

  0 1 2 3 4 5
0 0 1 1 0 0 1
1 1 0 1 1 0 0
2 1 1 0 1 0 1
3 0 1 1 0 1 0
4 0 0 0 1 0 1
5 1 0 1 0 1 0

In BFS we travel as wide as we can, using a Queue to mark the current Vertex’s children to keep the order to visit them. For the following animation, here are the first few steps:

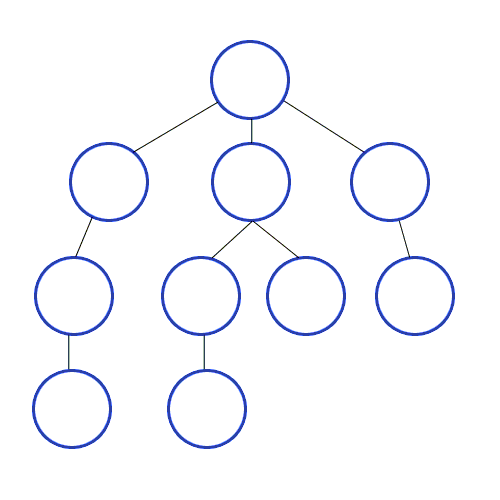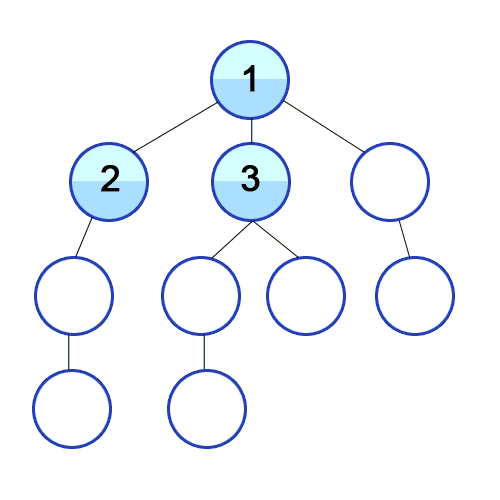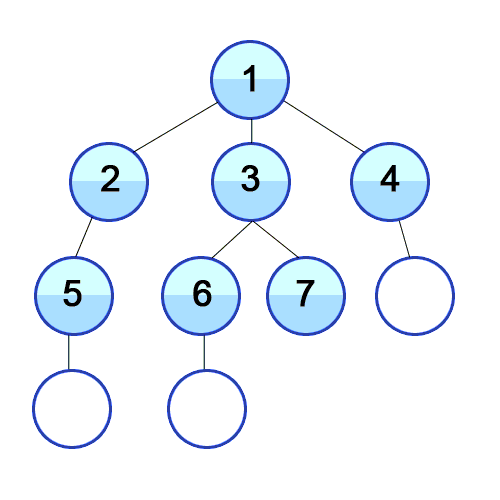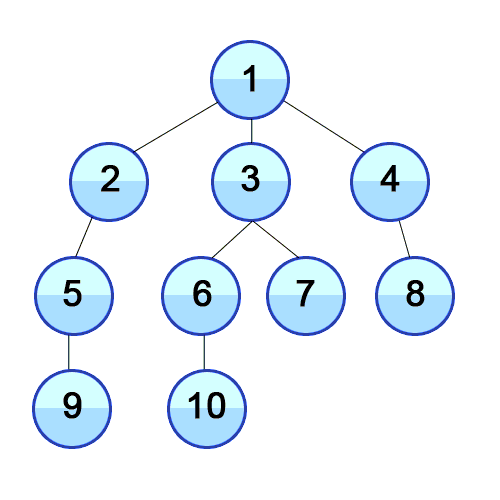
Why care about BFS? BFS is used to find the shortest path between two points (in unweighted undirected graphs, such as getting cellphone data from the closest cell tower), when buying flights to determine possible itineraries, finding relatives via DNA-sites (i.e., ancestry.com), web crawlers, and more!

In DFS we travel as deep down a path as we can, and upon hitting a dead end we backtrack as far as we need to hit another path. This process then repeats.

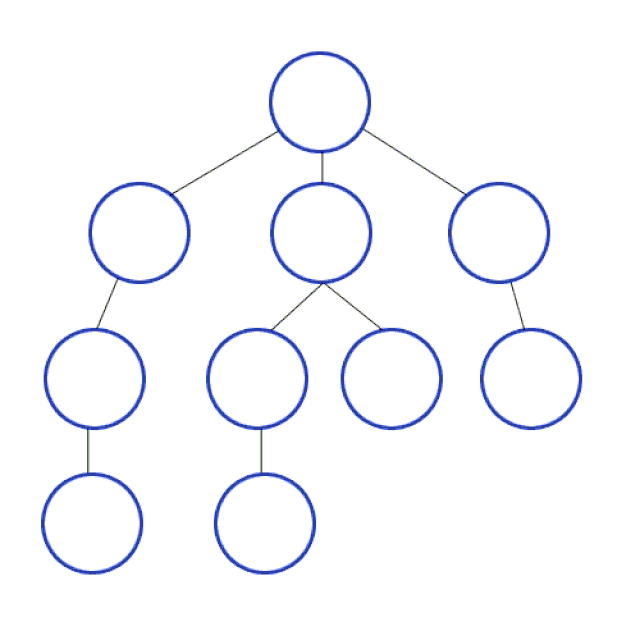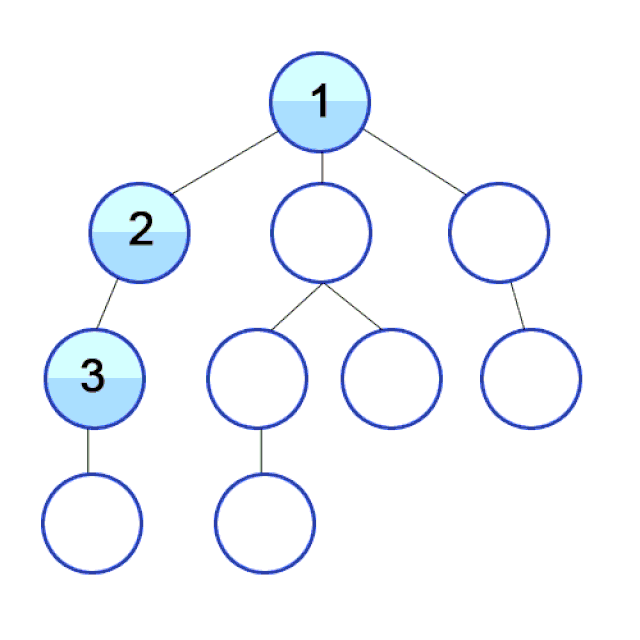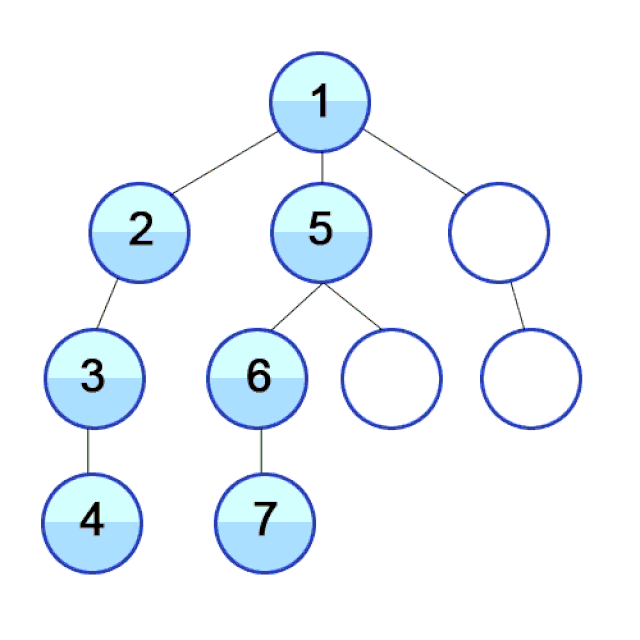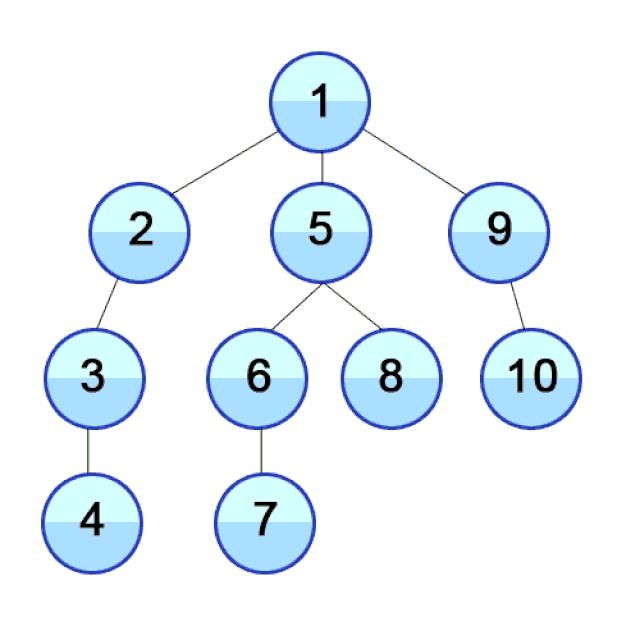
Why care about DFS? DFS is used to find the shortest path between two points (in weighted directed graphs, such as finding the fastest path to a location in traffic), solving mazes, web crawlers, robots that clean your floor, and more!

Your Task

Similar to last week’s lab, we give you a makefile, a unit test file, a doctest header file and a header file with class definitions for the Graphclass.

We have supplied graph.cpp to house your class definitions, and test.cpp will serve as your main file.

Thus you will need to follow the specifications in the next section very closely in order to complete the lab correctly.

The Graph Class

Since we are coding our graph as an Adjacency List, we have the following declared in our graph.h file:

std::vector<std::vector<std::pair<int,int>>> adj_list;

This is our 2D Vector of Pair objects, where each pair represents {destination, cost} as the demonstration above shows.

The rest of our Class consists of functions. Let’s go over them.

displayGraph()

Pretty self explanatory. It displays the graph. This function is complete and you do not need to touch it.

BFS(int vertex, std::ostream& os)

BFS helper function. Sets up what is needed to call the worker BFS that you will implement. This function is complete and you do not need to touch it.

DFS(int vertex, std::ostream& os)

DFS helper function. Sets up what is needed to call the worker DFS that you will implement. This function is complete and you do not need to touch it.

ensureValidGraph(int source, int destination)

This function is in place to make adding new Vertices easy. It ensures that adj_list is as long as it needs to be in order to represent the Vertices being added to the Graph. This should be called every time addEdge is called! Algorithm:

'l' = max(source, destination)
    
while 'adj_list' is smaller than the # of vertices we need:
	push an empty Vector of Pairs onto 'adj_list'
addEdge(int source, int destination, int cost)

Accepts a source, destination, and cost. Pushes a new Pair object into the correct location in adj_list. Algorithm:

ensure 'adj_list' is the correct size
create an edge from 'source' to 'destination' with the weight as 'cost'
create an edge from 'destination' to 'source' with the weight as 'cost'
BFS(std::queue &vertex_queue, std::vector &discovered, std::ostream& os)

Performs a Breadth-First Search starting from Vertex vertex and outputs the order that the Vertices are visited. Algorithm:

if 'vertex_queue' is empty:
	return

'current_vertex' = front of 'vertex_queue'
pop 'vertex_queue'
    
output 'vertex'
        
for each Pair 'p' in this Vertex:
	if 'p' has not been discovered:
		mark 'p' discovered
         	push 'p' into 'vertex_queue'
            
BFS('vertex_queue', 'discovered', 'os')
DFS(int vertex, std::vector &visited, std::ostream& os)

Performs a Depth-First Search starting from Vertex vertex and outputs the order that the Vertices are visited. Algorithm:

mark 'vertex' visited
output 'vertex'

for each Pair 'p' in this Vertex:
	if 'p' has not been visited
        	DFS('p', 'visited', os)

The Makefile

While you don’t necessarily need to know how it works, this file is what you will use for both compiling and running your code. The nice thing about a makefile is that if it is created correctly, all you need to do to compile your code is run the command make, no arguments needed. While this is the typical, most basic usage of a makefile, the makefile you are given goes one step further and runs your program immediately after compiling and then removes the binary it created.

Again, all you need to do is run make.

However, do be aware that until you have filled in your header file properly, your program will fail to compile and run. You should only concern yourself with trying to compile the program after implementing the contents of your header. Once you do, your program will compile, but it will still fail all of the tests. This is the point at which you should move on to implementing the methods.

The Unit Tests

The unit tests for this lab, found in test.cpp will perform various tests on each of your method implementations, giving you some feedback if a test fails. You shouldn’t need to do anything with this file, but you’re welcome to create additional test cases.

The Doctest Header

Don’t worry about doctest.h; for our purposes, it is magic.

Requirements

Your goal for this lab is to complete the following tasks in order:

  1. Why would we implement the Graph as an Adjacency List instead of as an Adjacency Matrix? Argue your case.
  2. Implement the adjacency list (ensureValidgraph() and addEdge())
  3. Implement BFS and DFS.

Stuck on #2? Check out this video

Handing in

Please call a TA over to get checked off before leaving your lab section (regardless of how far you got). If you want to continue working on your lab after your lab section, come to hours to get checked off.

Grade Breakdown

This assignment covers graphs and BFS & DFS and your level of knowledge on them will be assessed as follows:

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.