URI CSC 212 logo URI CSC 212

Lab 10

Binary Search Tree

On this page:
✔️ Motivation
✔️ Background Info
✔️ Your Task
✔️ Requirements
✔️ Handing in
✔️ Grade Breakdown

Motivation (Why are we doing this?)

The goal of this lab is to provide background to Binary Search Trees.

Background Info

A binary search tree is a data structure to store arbitrary “items” in a way that allows extremely rapid searches, insertion, and removal. They rely on sortable “keys” which are used to store and look up a given node. These “keys” and the way they are stored means that during a lookup, at each step, up to half of the entire tree can be discarded from the search.

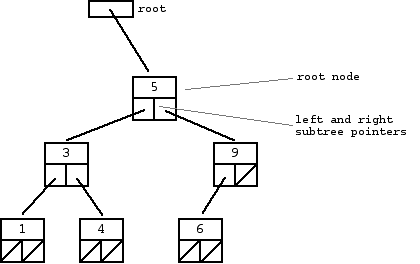
As you can see from the image above, a Binary Search Tree is ordered in the following way:

The resulting tree will have two subtrees stemming from the root node. The left-hand subtree will have key values which are all less than the root node’s key. The right-hand subtree will have key values which are all greater than the root node’s key.

Check out this binary search tree visualization from USFCA.

Aside from putting in the methods declarations, which will be explained in more detail below, you have the following to make your classes work properly:

Class Contents

In BSTNode:

In BSTree:

Constructor and Destructor

The constructor should take no parameters and initialize the root variable with an appropriate value. In other words, it should create an empty tree.

The destructor should delete the entire tree, which is an operation best performed recursively. However, destructors in C++ cannot be recursive. The solution to this predicament is to use a private helper method, destroy(), which will be described in further detail below. The destructor should just call destroy(), passing in the root node pointer.

Note: A common theme in many of these methods is to have a public, non-recursive method which simply calls a private, recursive function on the root node. This is because a binary search tree can be traversed or searched easily by calling a recursive method on a node’s left child, right child or both. In fact, due to a concept called function overloading, these methods can have the same name so long as they have different parameters.

It is recommended to work on these methods in order and test them using make before moving on to the next. Don’t be alarmed– more info on make is available further into the reading.

Insert

You should create two methods named insert(), one which takes an integer and returns nothing, and the other which takes a BSTNode * and an integer and returns a BSTNode *. The first method is the public method, which the user will be able to call, and the second method is the private recursive method which actually inserts the node in the correct place in the tree.

Height

Again, create two methods named height(), one private and one public. The public method should take no parameters, call the private method on the root, and return the resulting integer representing the height of the tree. The private method should take a BSTNode * parameter and return an integer representing the height of the subtree rooted at the node passed in.

Note: Calling the height method on an empty tree should return -1 as a tree with one node is of height 0. The -1 is used to distinguish between the two.

Traversals

Here you will need six methods in total:

  1. Two preorder() methods: one private and one public
  2. Two inorder() methods: one private and one public
  3. Two postorder() methods: one private and one public

Each public method should take the line std::ostream& os = std::cout as a parameter and return void, simply calling the private counterpart with the root node pointer and the ostream.

Each private method should take a BSTNode * and a std::ostream& as parameters and return void, performing the traversal specified by its name.

The ostream is needed solely for testing, but you can also think of it as a generalization of printing. Instead of writing data to STDOUT using std::cout, you will instead write to the ostream passed in as an argument. Thus, when you visit each node, you should write its data to the ostream just as you would with cout, including the std::endl.

As for the parameter std::ostream& os = std::cout, this allows you to call the method without passing in an ostream, in which case the method will use cout by default.

Essentially, calling the method as traversal() will default to using std::cout, and outputting as os << "anything" will work exactly as you’d expect std::cout << "anything" to work.

Destroy

You should create a destroy function which is private and takes a node and returns void. It should destroy the entire subtree starting at node recursively.

Ensure that you only delete your current node after all subtrees have been freed (otherwise you’ll have a memory leak!). HINT: Think about which type of traversal would be best to implement this method.

You should create a public search method which takes an integer and returns a boolean indicating whether or not the node was found. It should search the tree recursively and return true if and only if the value is found, false otherwise.

Your Task

This lab is a bit different compared to previous labs in that you will be exposed to some new concepts. To be more specific, we give you a makefile, a unit test file, a doctest header file and a header file with class definitions for BSTNode and BSTree classes (plus a couple other things). We have supplied bst.cpp to house your class definitions, and test.cpp will serve as your main file.

Thus you will need to follow the specifications in the next section very closely in order to complete the lab correctly.

The BST Header

If you take a look into bst.h, you will notice that it has been pre-written for you. It also contains some code you’ve likely never seen before, like the following:

#ifndef MAX
#define MAX(a,b) ((a > b) ? a : b)
#endif

Similarly to the preprocessor directive defining NULL, this statement defines a macro which actually takes arguments. This allows the preprocessor to replace any instance of MAX(a,b) with ((a > b) ? a : b), which is just a convenient way of getting the max of two numbers, a and b, without even needing to create a function.

All that remains then is the class definitions. For the sake of completeness, BSTNode is the class which will be used for each node of the tree, and BSTree is the class for the tree itself. What you actually need to do with these classes will be explained in the next section.

The Makefile

While you don’t necessarily need to know how it works, this file is what you will use for both compiling and running your code. The nice thing about a makefile is that if it is created correctly, all you need to do to compile your code is run the command make, no arguments needed. While this is the typical, most basic usage of a makefile, the makefile you are given goes one step further and runs your program immediately after compiling and then removes the binary it created.

Again, all you need to do is run make.

However, do be aware that until you have filled in your header file properly, your program will fail to compile and run. You should only concern yourself with trying to compile the program after implementing the contents of your header. Once you do, your program will compile, but it will still fail all of the tests. This is the point at which you should move on to implementing the methods.

The Unit Tests

The unit tests for this lab, found in test.cpp will perform various tests on each of your method implementations, giving you some feedback if a test fails. You shouldn’t need to do anything with this file, but you’re welcome to create additional test cases.

The Doctest Header

Don’t worry about doctest.h; for our purposes, it is magic.

Hint: The unit tests for insert() and height() rely on one another, so they both need to be implemented correctly before you can pass either method’s test cases.

Requirements

Your goal for this lab is to complete the following tasks in order:

  1. Comment all of the functions in “bst.cpp” with your strategy for implementing them
  2. Implement the following:
    1. The Constructors
    2. The Destructors
    3. preorder()
    4. postorder()
    5. inorder()
  3. Implement the following:
    1. height()
    2. insert()
    3. search()
  4. Implement and test the following:
    1. isComplete() which tells us if the tree is complete
    2. isFull() which tells us if the tree is full

HINT 1: Some of these will be very similar and some will be identical to your binary tree implementation from last week’s lab! Others won’t. Think about the differences between a BT and a BST and use that to guide your implementation.
HINT 2: Review Lab 9 to review the definitions of a complete and full tree for #4.
HINT 3: For #4, there is a relationship between how far down the tree you are and the # of total nodes in the tree to determine completeness.
HINT 4: For #4, you’ll need to create new test cases in test.cpp. Insert -> Perfect should return True for isFull(), and you can easily modify that case to test for isComplete().

Handing in

Please call a TA over to get checked off before leaving your lab section (regardless of how far you got). If you want to continue working on your lab after your lab section, come to hours to get checked off.

Grade Breakdown

This assignment covers Binary Search Trees (Implementation) and Binary Search and your level of knowledge on them will be assessed as follows:

We’re not asking for delete() but if you want to challenge yourself, you’re welcome to implement it as well!

To receive any credit at all, you must abide by our Collaboration and Academic Honesty Policy. Failure to do so may result in a failing grade in the class and/or further disciplinary action.

Original assignment by Dr. Marco Alvarez, used and modified with permission.